题目内容
(本小题满分13分)
在数列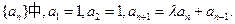
(I)若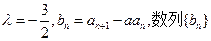 是公比为β的等比数列,求α和β的值。
是公比为β的等比数列,求α和β的值。
(II)若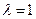 ,基于事实:如果d是a和b的公约数,那么d一定是a-b的约数。研讨是否存在正整数k和n,使得
,基于事实:如果d是a和b的公约数,那么d一定是a-b的约数。研讨是否存在正整数k和n,使得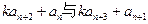 有大于1的公约数,如果存在求出k和n,如果不存在请说明理由。
有大于1的公约数,如果存在求出k和n,如果不存在请说明理由。
在数列
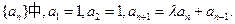
(I)若
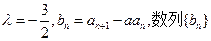 是公比为β的等比数列,求α和β的值。
是公比为β的等比数列,求α和β的值。(II)若
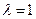 ,基于事实:如果d是a和b的公约数,那么d一定是a-b的约数。研讨是否存在正整数k和n,使得
,基于事实:如果d是a和b的公约数,那么d一定是a-b的约数。研讨是否存在正整数k和n,使得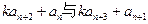 有大于1的公约数,如果存在求出k和n,如果不存在请说明理由。
有大于1的公约数,如果存在求出k和n,如果不存在请说明理由。(1)
 或
或 …
…(2)故不存在
 使
使 与
与 有大于1的公约数.
有大于1的公约数.(I) 是公比的
是公比的 的等比数列
的等比数列

 …………2分
…………2分
即
又
 ………………4分
………………4分
 、
、 是方
是方 程
程 的两根
的两根
 或
或 …………6分
…………6分
(II)假设存在正整数 ,
, 使得
使得 与
与 有大于1的公约数
有大于1的公约数
 ,
,
则 也是
也是 即
即 的约数
的约数
依题设 ,
,
 是
是 的约数…………8分
的约数…………8分
从而 是
是 与
与 的公约数
的公约数
同理可得 是
是 的约数依次类推,
的约数依次类推, 是
是 与
与 的约数……10分
的约数……10分
 ,故
,故
于是
 ………………12分
………………12分
又∵
 是
是 的约数和
的约数和 的约数
的约数
 是
是 即
即 的约数
的约数
从而 是
是 即1的约数,这与
即1的约数,这与 矛盾
矛盾
故不存在 使
使 与
与 有大于1的公约数.
有大于1的公约数.
 是公比的
是公比的 的等比数列
的等比数列
 …………2分
…………2分即

又

 ………………4分
………………4分 、
、 是方
是方 程
程 的两根
的两根 或
或 …………6分
…………6分(II)假设存在正整数
 ,
, 使得
使得 与
与 有大于1的公约数
有大于1的公约数
 ,
,则
 也是
也是 即
即 的约数
的约数依题设
 ,
,
 是
是 的约数…………8分
的约数…………8分从而
 是
是 与
与 的公约数
的公约数同理可得
 是
是 的约数依次类推,
的约数依次类推, 是
是 与
与 的约数……10分
的约数……10分 ,故
,故
于是

 ………………12分
………………12分又∵

 是
是 的约数和
的约数和 的约数
的约数 是
是 即
即 的约数
的约数从而
 是
是 即1的约数,这与
即1的约数,这与 矛盾
矛盾故不存在
 使
使 与
与 有大于1的公约数.
有大于1的公约数.
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 ( )
( )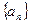 的各项都为正数,
的各项都为正数,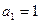 ,前
,前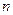 项和
项和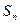 满足
满足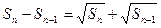 (
(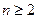 ).
).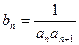 (
(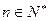 ),数列
),数列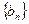 的前
的前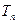 ,若
,若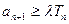 对任意正整数
对任意正整数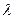 的取值范围.
的取值范围. 各项均不为0,其前
各项均不为0,其前 项和为
项和为 ,且对任意
,且对任意 都有
都有 (
( 为大于1的常数),记f(n)
为大于1的常数),记f(n) .
. ;
; 与
与 的大小(
的大小(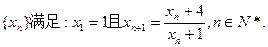
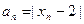 ,Sn为数列{an}前n项和,求证:当
,Sn为数列{an}前n项和,求证:当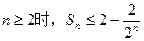 .
. }的前 n项和,求 Tn
}的前 n项和,求 Tn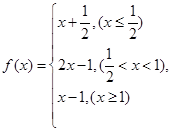
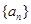 满足
满足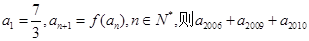 =
= 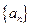 是公差不为零
是公差不为零 的等差数列,前
的等差数列,前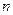 项和为
项和为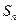 ,
,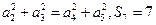 ,则使得
,则使得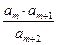 为数列
为数列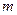 的值为
的值为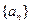 的前
的前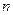 项和为
项和为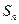 .若
.若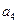 是
是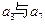 的等比中项,
的等比中项, 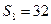 ,则
,则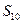 等于( )
等于( )