题目内容
(本题满分12分)
已知数列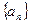 的各项都为正数,
的各项都为正数,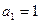 ,前
,前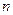 项和
项和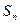 满足
满足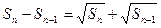 (
(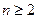 ).
).
(Ⅰ)求数列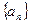 的通项公式;
的通项公式;
(Ⅱ)令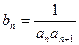 (
(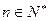 ),数列
),数列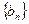 的前
的前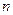 项和为
项和为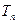 ,若
,若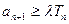 对任意正整数
对任意正整数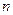 都成立,求实数
都成立,求实数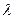 的取值范围.
的取值范围.
已知数列
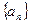 的各项都为正数,
的各项都为正数,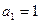 ,前
,前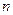 项和
项和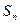 满足
满足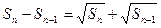 (
(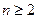 ).
).(Ⅰ)求数列
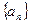 的通项公式;
的通项公式;(Ⅱ)令
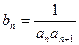 (
(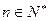 ),数列
),数列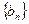 的前
的前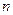 项和为
项和为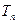 ,若
,若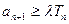 对任意正整数
对任意正整数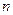 都成立,求实数
都成立,求实数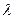 的取值范围.
的取值范围.(Ⅰ)
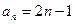
(Ⅱ)
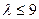
解:(Ⅰ)∵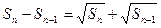 ,
,
∴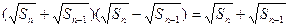 ,
,
又∵ ,∴
,∴ ,
,
∴ (
(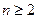 ),
),
∴数列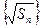 是等差数列,首项为
是等差数列,首项为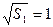 ,公差为1,
,公差为1,
∴ ,∴
,∴
当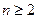 时,
时,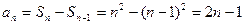 ;
;
又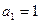 ,
,
∴数列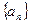 的通项公式为
的通项公式为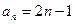 .
.
(Ⅱ) ,
,
∴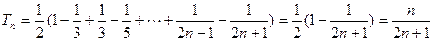 .
.
由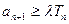 得
得 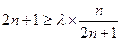 对任意正整数
对任意正整数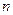 都成立,
都成立,
∴ ,∴
,∴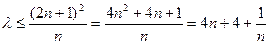 .
.
令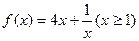 ,则
,则 ,
,
∴ 在
在 上递增,∴对任意正整数
上递增,∴对任意正整数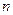 ,
, 的最小值为5,
的最小值为5,
∴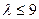
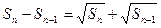 ,
,∴
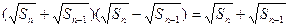 ,
,又∵
 ,∴
,∴ ,
,∴
 (
(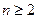 ),
),∴数列
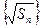 是等差数列,首项为
是等差数列,首项为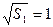 ,公差为1,
,公差为1,∴
 ,∴
,∴
当
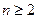 时,
时,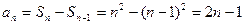 ;
;又
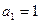 ,
,∴数列
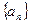 的通项公式为
的通项公式为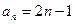 .
.(Ⅱ)
 ,
,∴
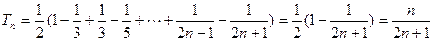 .
. 由
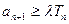 得
得 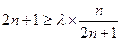 对任意正整数
对任意正整数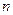 都成立,
都成立,∴
 ,∴
,∴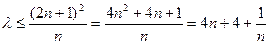 .
. 令
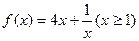 ,则
,则 ,
,
∴
 在
在 上递增,∴对任意正整数
上递增,∴对任意正整数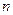 ,
, 的最小值为5,
的最小值为5,∴
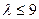

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
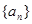 是等差数列,如果
是等差数列,如果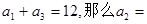 ( )
( )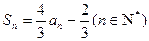 ,求数列
,求数列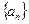 的通项公式(6分);
的通项公式(6分);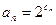 ,求证数列
,求证数列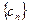 是一个 “1类和科比数列”(4分);
是一个 “1类和科比数列”(4分);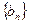 是一个 “
是一个 “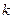 类和科比数列”,其中首项
类和科比数列”,其中首项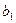 ,公差
,公差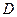 ,探究
,探究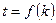 (6分);
(6分);
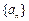 中,
中,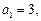
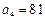
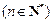 .
.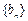 为等差数列,且满足
为等差数列,且满足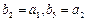 ,求数列
,求数列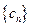 满足
满足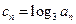 ,求数列
,求数列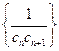 的前
的前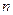 项和
项和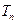 .
.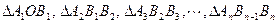 均为等腰直角三角形, 已知它们的直角顶点
均为等腰直角三角形, 已知它们的直角顶点 …,
…, 在曲线
在曲线 上,
上, 在
在 轴上(如图),
轴上(如图),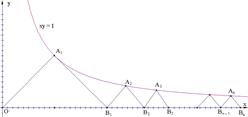
 的长;
的长; 的通项公式.
的通项公式. 中,
中,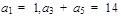 ,其前n项和
,其前n项和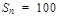 ,则n等于( )
,则n等于( )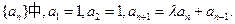
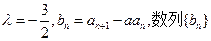 是公比为β的等比数列,求α和β的值。
是公比为β的等比数列,求α和β的值。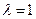 ,基于事实:如果d是a和b的公约数,那么d一定是a-b的约数。研讨是否存在正整数k和n,使得
,基于事实:如果d是a和b的公约数,那么d一定是a-b的约数。研讨是否存在正整数k和n,使得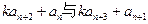 有大于1的公约数,如果存在求出k和n,如果不存在请说明理由。
有大于1的公约数,如果存在求出k和n,如果不存在请说明理由。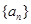 满足
满足 ,则
,则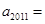 ( )
( ) B
B  C
C  D
D 
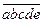 称为“凸”数,当且仅当它满足a<b<c,c>d>e(如12430,13531等), 则在所有的五位数中“凸”数的个数是( ▲ )
称为“凸”数,当且仅当它满足a<b<c,c>d>e(如12430,13531等), 则在所有的五位数中“凸”数的个数是( ▲ )