题目内容
【题目】已知A(4,-3),B(2,-1)和直线l:4x+3y-2=0.
(1)求在直角坐标平面内满足|PA|=|PB|的点P的方程;
(2)求在直角坐标平面内一点P满足|PA|=|PB|且点P到直线l的距离为2的坐标.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由题意可知|PA|=|PB|即点P为线段AB的中垂线,所过点P的轨迹为过AB中点,斜率满足![]() 。(2)由(1)可知点P的方程x-y-5=0,
。(2)由(1)可知点P的方程x-y-5=0,
设点P的坐标为(a,b),再由点到直线的距离公式和点在直线x-y-5=0,列方程组可解。
试题解析:(1)∵A(4,-3),B(2,-1),
∴线段AB的中点M的坐标为(3,-2),又![]()
∴线段AB的垂直平分线方程为y+2=x-3,
即点P的方程x-y-5=0.
(2)设点P的坐标为(a,b),
∵点P(a,b)在上述直线上,∴a-b-5=0.①
又点P(a,b)到直线l:4x+3y-2=0的距离为2,
∴![]() =2,即4a+3b-2=±10,②
=2,即4a+3b-2=±10,②
联立①②可得![]() 或
或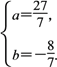
∴所求点P的坐标为(1,-4)或![]() .
.

练习册系列答案
相关题目