题目内容
【题目】已知F1，F2分别是双曲线
的左、右焦点，若F2关于渐近线的对称点恰落在以F1为圆心
为半径的圆上，则双曲线C的离心率为 _____．
【答案】2
【解析】
首先求出F2到渐近线的距离，利用F2关于渐近线的对称点恰落在以F1为圆心，|OF1|为半径的圆上，可得直角三角形，即可求出双曲线的离心率．
由题意，设双曲线的方程为
，
F1（﹣c，0），F2（c，0），
设一条渐近线方程为y=
x，
则F2到渐近线的距离为 
=b．
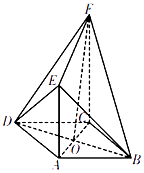
设F2关于渐近线的对称点为P，F2P与渐近线交于A，
可得|PF2|=2b，A为F2P的中点，
又O是F1F2的中点，∴OA∥F1P，则∠F1PF2为直角，
由△PF1F2为直角三角形，
由勾股定理得4c2=c2+4b2
即有3c2=4（c2﹣a2），即为c2=4a2，
即c=2a，则e=
=2．
故为：2.
练习册系列答案
相关题目
