Question

【题目】已知函数

（Ⅰ）若函数在上为增函数，求正实数的取值范围；

（Ⅱ）若关于的方程在区间内恰有两个相异的实根，求实数的取值范围．

Answer 1

【答案】（Ⅰ）;（Ⅱ）.

【解析】分析：（Ⅰ）先求出函数的增区间为， 应为其子集，故可求实数的范围.

（Ⅱ）方程在上有两个实数根可以转化为直线与函数的图像有两个不同的交点，利用导数刻画的图像后可以得到实数的取值范围.

详解：（Ⅰ） ，

因为为正实数，由定义域知，所以函数的单调递增区间为.

因为函数在上为增函数，所以，所以.

（Ⅱ）因为方程在区间内恰有两个相异的实根，故

方程在区间内恰有两个相异的实根即

方程在区间内恰有两个相异的实根.

令，则，

当时， ， 在为减函数；

当时， ， 在为增函数.

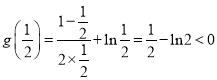
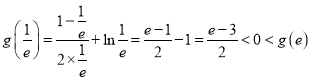
的图像如图所示：

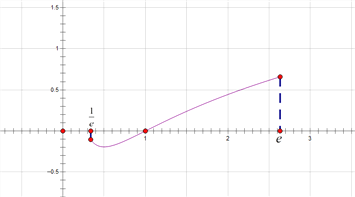
要使函数的图象与函数的图象在区间内恰有两个交点，则要满足，所以的取值范围为.