Question

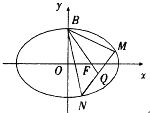
【题目】已知椭圆 （a＞b＞0）的一个顶点为B（0，4），离心率e= ，直线l交椭圆于M，N两点．
（1）若直线l的方程为y=x﹣4，求弦MN的长；
（2）如果△BMN的重心恰好为椭圆的右焦点F，求直线l方程的一般式．

Answer 1

【答案】
（1）

解：由已知椭圆 （a＞b＞0）的一个顶点为B（0，4），

∴b=4，

又∵离心率e= ，

即 ，

∴ ，解得a2=20，

∴椭圆方程为 ；

由4x2+5y2=80与y=x﹣4联立，

消去y得9x2﹣40x=0，

∴x1=0， ，

∴所求弦长

（2）

解：椭圆右焦点F的坐标为（2，0），

设线段MN的中点为Q（x0，y0），

由三角形重心的性质知 ，又B（0，4），

∴（2．﹣4）=2（x0﹣2，y0），

故得x0=3，y0=﹣2，

求得Q的坐标为（3，﹣2）；

设M（x1，y1），N（x2，y2），则x1+x2=6，y1+y2=﹣4，

且 ，

以上两式相减得 ，

∴ ，

故直线MN的方程为 ，即6x﹣5y﹣28=0．

【解析】（1）由已知中椭圆 （a＞b＞0）的一个顶点为B（0，4），离心率e= ，根据e= ，b=4，a2=b2+c2可求出椭圆的标准方程，进而求直线l的方程及弦长公式，得到弦MN的长；（2）设线段MN的中点为Q（x0 ， y0），结合（1）中结论，及△BMN的重心恰好为椭圆的右焦点F，由重心坐标公式，可得Q点坐标，由中点公式及M，N也在椭圆上，求出MN的斜率，可得直线l方程．