题目内容
设数列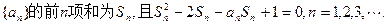
(1)求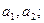
(2)求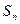 的表达式.
的表达式.
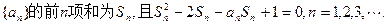
(1)求
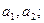
|
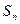 的表达式.
的表达式.(1)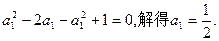
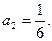
(2)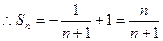
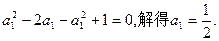
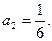
(2)
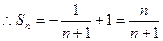
解:(1)当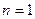 时,由已知得
时,由已知得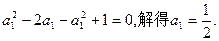
同理,可解得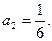 4分
4分
(2)解法一:由题设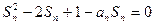 当
当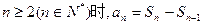
代入上式,得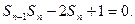 (*) 6分
(*) 6分
由(1)可得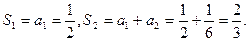 由(*)式可得
由(*)式可得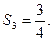
由此猜想: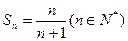 8分
8分
证明:①当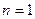 时,结论成立.②假设当
时,结论成立.②假设当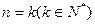 时结论成立,
时结论成立,
即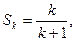 那么,由(*)得
那么,由(*)得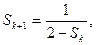
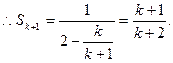
所以当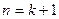 时结论也成立,根据①和②可知,
时结论也成立,根据①和②可知,
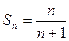 对所有正整数n都成立.因
对所有正整数n都成立.因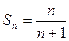 12分
12分
解法二:由题设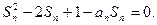 当
当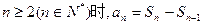
代入上式,得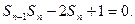
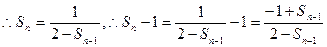
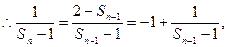
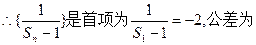 -1的等差数列,
-1的等差数列,
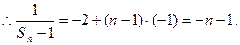
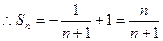 12分
12分
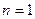 时,由已知得
时,由已知得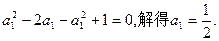
同理,可解得
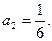 4分
4分(2)解法一:由题设
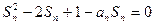 当
当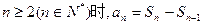
代入上式,得
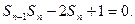 (*) 6分
(*) 6分由(1)可得
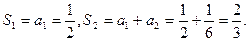 由(*)式可得
由(*)式可得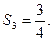
由此猜想:
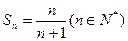 8分
8分证明:①当
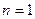 时,结论成立.②假设当
时,结论成立.②假设当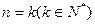 时结论成立,
时结论成立,即
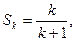 那么,由(*)得
那么,由(*)得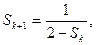
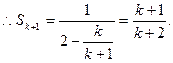
所以当
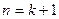 时结论也成立,根据①和②可知,
时结论也成立,根据①和②可知,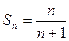 对所有正整数n都成立.因
对所有正整数n都成立.因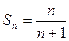 12分
12分解法二:由题设
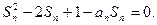 当
当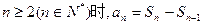
代入上式,得
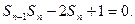
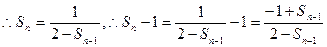
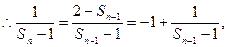
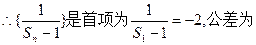 -1的等差数列,
-1的等差数列,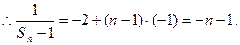
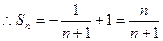 12分
12分
练习册系列答案
相关题目
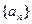 是首项
是首项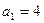 的等比数列,其前
的等比数列,其前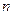 项和为Sn,且
项和为Sn,且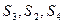 成等比数列.
成等比数列.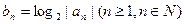 ,设
,设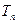 为数列
为数列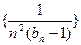 的前
的前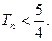
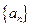 满足
满足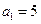 ,
, 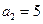 ,
,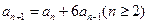 .
.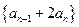 是等比数列
是等比数列 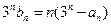 ,且
,且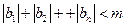 对于
对于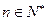 恒成立,求
恒成立,求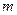 的取值范围
的取值范围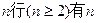 个数,且两端的数都是
个数,且两端的数都是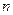 ,其余的每一个数都等于它肩上两个数的和,则第
,其余的每一个数都等于它肩上两个数的和,则第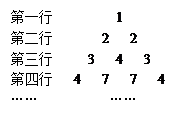
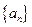 的前
的前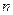 项和
项和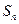 满足
满足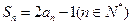 ,那么数列
,那么数列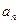 = .
= .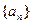 中,
中,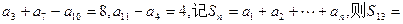
 78
78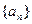 中,
中,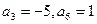 ,此数列的通项公式为 ,设
,此数列的通项公式为 ,设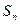 是数列
是数列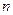 项和,则
项和,则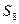 等于 。
等于 。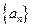 满足
满足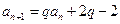 (
(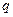 为常数,
为常数,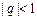 ),若
),若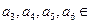
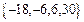 ,则
,则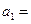 ▲ .
▲ .