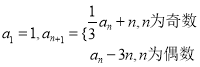题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(2)若关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,求实数
,求实数![]() 、
、![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ,
, ![]() .
.
【解析】试题分析:(1) ![]() 时,
时, ![]() ,化为
,化为![]() ,计算得出即可;(2)利用一元二次不等式的解集与相应的一元二次方程的实数根的关系即可得出.
,计算得出即可;(2)利用一元二次不等式的解集与相应的一元二次方程的实数根的关系即可得出.
试题解析:(1)由已知有: ![]() ,
,
即![]() ,解得:
,解得: ![]() .所以不等式的解集为:
.所以不等式的解集为: ![]()
(2)由关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() 可知:
可知:
![]() ,3是关于
,3是关于![]() 的方程
的方程![]() 的两个根,则有
的两个根,则有
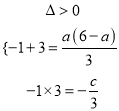
解得: ![]() ,
, ![]()
点晴:本题考查的是二次函数,二次方程,二次不等式三个二次之间的关系.解决本题的关键是弄清楚函数的零点,方程的根,不等式解集的端点之间的对应关系,一方面结合韦达定理可求出各系数;另一方面结合二次系数的正负确定函数的开口方向,不等式的解集取中间还是两边.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目