题目内容
已知:在函数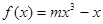 的图象上,以
的图象上,以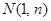 为切点的切线的倾斜角为
为切点的切线的倾斜角为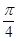 .
.
(Ⅰ)求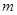 ,
,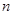 的值;
的值;
(Ⅱ)是否存在最小的正整数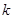 ,使得不等式
,使得不等式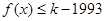 对于
对于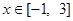 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数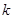 ;如果不存在,请说明理由;
;如果不存在,请说明理由;
(Ⅲ)求证: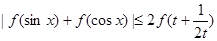 (
(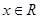 ,
,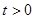 ).
).
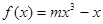 的图象上,以
的图象上,以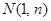 为切点的切线的倾斜角为
为切点的切线的倾斜角为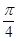 .
.(Ⅰ)求
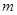 ,
,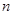 的值;
的值;(Ⅱ)是否存在最小的正整数
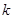 ,使得不等式
,使得不等式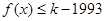 对于
对于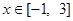 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数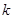 ;如果不存在,请说明理由;
;如果不存在,请说明理由;(Ⅲ)求证:
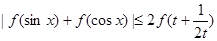 (
(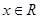 ,
,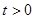 ).
).(Ⅰ) .
.
(Ⅱ)存在最小的正整数 ,使得不等式
,使得不等式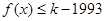 对于
对于 恒成立.
恒成立.
(Ⅲ)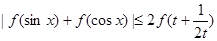 (
(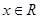 ,
,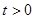 ).
).
 .
. (Ⅱ)存在最小的正整数
 ,使得不等式
,使得不等式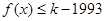 对于
对于 恒成立.
恒成立.(Ⅲ)
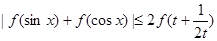 (
(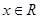 ,
,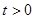 ).
). 试题分析:(Ⅰ)
 ,依题意,得
,依题意,得
 ,即
,即 ,
, .
.2分
∵
 , ∴
, ∴  . 3分
. 3分(Ⅱ)令
 ,得
,得 . 4分
. 4分当
 时,
时, ;
;当
 时,
时, ;
;当
 时,
时, .
.又
 ,
, ,
, ,
, .
.因此,当
 时,
时, . 7分
. 7分要使得不等式
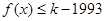 对于
对于 恒成立,则
恒成立,则 .
.所以,存在最小的正整数
 ,使得不等式
,使得不等式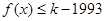 对于
对于 恒成立. 9分
恒成立. 9分(Ⅲ)方法一:





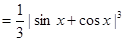

 . 11分
. 11分又∵
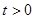 ,∴
,∴  ,
, .
.∴
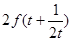


 . 13分
. 13分综上可得,
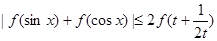 (
(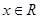 ,
,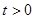 ). 14分
). 14分方法二:由(Ⅱ)知,函数
 在 [-1,
在 [-1, ]上是增函数;在[
]上是增函数;在[ ,
, ]上是减函数;在[
]上是减函数;在[ ,1]上是增函数.
,1]上是增函数.又
 ,
, ,
, ,
, .
.所以,当x∈[-1,1]时,
 ,即
,即 .
.∵
 ,
, ∈[-1,1],∴
∈[-1,1],∴  ,
, .
.∴
 . 11分
. 11分又∵
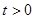 ,∴
,∴  ,且函数
,且函数 在
在 上是增函数.
上是增函数.∴
 . 13分
. 13分综上可得,
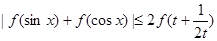 (
(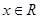 ,
,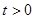 ). 14分
). 14分点评:难题,本题综合性较强,对复杂式子的变形能力要求较高。不等式的证明中,灵活运用不等式的性质是一个关键点。

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 与函数
与函数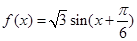 与
与 的图像分别交于
的图像分别交于 两点,则
两点,则 的最大值为 .
的最大值为 . 和
和 (其中
(其中 ),
), 与函数
与函数 的图像从左至右相交于点
的图像从左至右相交于点 ,
, ,
, 与函数
与函数 ,
, .记线段
.记线段 和
和 在
在 轴上的投影长度分别为
轴上的投影长度分别为 .当
.当 变化时,
变化时, 的最小值为( )
的最小值为( )



 .
.  ;
;  ,求证:
,求证: ≤
≤ .
.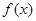 是定义在
是定义在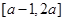 上的偶函数,且当
上的偶函数,且当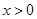 时,
时,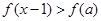 的解集为 ( )
的解集为 ( )

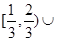
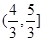
 的单调增区间是_________
的单调增区间是_________ 是以
是以 为周期的偶函数,当
为周期的偶函数,当 时,
时, .若关于
.若关于 的方程
的方程 (
( )在区间
)在区间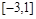 内有四个不同的实根,则
内有四个不同的实根,则 的取值范围是
的取值范围是


