题目内容
14.如果f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(-x)成立,则称此函数具有“P(a)性质”,给出下列命题:①函数y=sinx具有“P(a)性质”;
②若奇函数y=f(x)具有“P(2)性质”,且f(1)=1,则f(2015)=1;
③若不恒为零的函数y=f(x)同时具有“P(0)性质”和“P(3)性质”,则函数y=f(x)是周期函数;
④若函数y=f(x)具有“P(4)性质”,图象关于点(1,0)成中心对称,且在(-1,0)上单调递减,则y=f(x)在(-2,-1)上单调递减,在(1,2)上单调递增;
其中正确的是①③④(写出所有正确命题的编号).
分析 由条件:f(x+a)=f(-x)成立可得:函数f(x)的图象关于直线x=$\frac{a}{2}$对称,是轴对称图形,
①根据正弦函数的对称轴即可判断;
②由“P(2)性质”得:f(x+2)=f(-x),由奇函数的性质推出函数的周期,由周期性求出f(2015)的值;
③由“P(0)性质”和“P(3)性质”列出等式,即可求出函数的周期;
④由“P(4)性质”得f(x+4)=f(-x),则f(x)关于x=2对称,即f(2-x)=f(2+x),由偶函数的性质和图象关于点(-1,0)成中心对称,即可得到答案.
解答 解:若对于定义域内的任意x,存在实数a使得f(x+a)=f(-x)成立,
则函数f(x)的图象关于直线x=$\frac{a}{2}$对称,是轴对称图形,
①函数y=sinx的对称轴是x=$\frac{π}{2}+kπ(k∈Z)$,则具有“P(a)性质”,①正确;
②若奇函数y=f(x)具有“P(2)性质”,则f(x+2)=f(-x)=-f(x),
所以f(x+4)=f(x),函数f(x)的周期是4,
由f(1)=1得,f(2015)=f(4×504-1)=f(-1)=-f(1)=-1,②不正确;
③∵恒为零的函数y=f(x)同时具有“P(0)性质”和“P(3)性质”,
∴f(x)=f(-x),f(x+3)=f(-x)=f(x),
∴f(x)为偶函数,且周期为3,③正确;
④∵函数y=f(x)具有“P(4)性质”,则f(x+4)=f(-x),
∴f(x)关于x=2对称,即f(2-x)=f(2+x),
∵图象关于点(1,0)成中心对称,
∴f(2-x)=-f(x),即f(2+x)=-f(-x),
则f(x)=f(-x),即f(x)为偶函数,
∵图象关于点(1,0)成中心对称,且在(-1,0)上单调递减,
∴图象也关于点(-1,0)成中心对称,且在(-2,-1)上单调递减,
根据偶函数的对称得出:在(1,2)上单调递增,④正确,
故答案为:①③④.
点评 本题考是新概念的题目,考查函数的奇偶性、周期性、单调性、对称性的综合应用,主要运用抽象函数性质进行推理判断,难度较大,属于中档题.

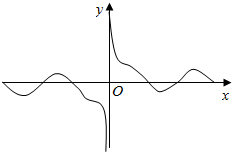 如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g(x)=$\frac{1}{x}$,则Q(x)是( )
如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g(x)=$\frac{1}{x}$,则Q(x)是( )| A. | $\frac{f(x)}{g(x)}$ | B. | f (x)g (x) | C. | f (x)-g(x) | D. | f(x)+g(x) |
| A. | 1-i | B. | 1+i | C. | 2+i | D. | 2-i |
| A. | 78 | B. | 91 | C. | 39 | D. | 2015 |
| A. | $({\frac{1}{2},2})$ | B. | (-1,2) | C. | $[{\frac{1}{2},2}]$ | D. | [-1,2] |
| A. | 2+i | B. | 2-i | C. | $\frac{10}{3}$+$\frac{5}{3}$ | D. | $\frac{10}{3}$$-\frac{5}{3}$ |