设Sn为等差数列{an}的前n项和.且a1-a7+a13=6.则S13=( )A．78B．91C．39D．2015 题目和参考答案——青夏教育精英家教网—

题目内容

9．设S_n为等差数列{a_n}的前n项和，且a₁-a₇+a₁₃=6，则S₁₃=（　　）

A．

B．

C．

D．

2015

分析在等差数列{a_n}中，由a₁-a₇+a₁₃=6，解得a₇=6，再由等差数列的通项公式和前n项和公式能求出S₁₃的值．

解答解：等差数列{a_n}中，
∵a₁-a₇+a₁₃=6，
∴2a₇-a₇=6，解得a₇=6．
∴S₁₃=$\frac{13（{a}_{1}+{a}_{13}）}{2}=\frac{13×2{a}_{7}}{2}=13{a}_{7}=78$．
故选：A．

点评本题考查了等差数列的性质，灵活运用等差数列的前n项和的公式化简求值，是一道基础题．

练习册系列答案

相关题目

15．当m取不同的有理数时，讨论幂函数y=x^m的定义域．

16．若满足c=2，面积S=$\frac{1}{2}$$\overrightarrow{CA}$•$\overrightarrow{CB}$的△ABC有两个，则边长BC的取值范围是（2，2$\sqrt{2}$）．

17．

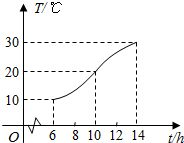如图，某地一天中6时至14时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b（其中$\frac{π}{2}＜φ＜π$），与图中曲线对应的函数解析式是$y=10sin（\frac{π}{8}x+\frac{3π}{4}）+20，x∈[{6，14}]$．

4．设集合A={x|3＜x＜7，x∈Z }，B={x|4＜x＜8，x∈N }，则A∩B=（　　）

14．如果f（x）的定义域为R，对于定义域内的任意x，存在实数a使得f（x+a）=f（-x）成立，则称此函数具有“P（a）性质”，给出下列命题：
①函数y=sinx具有“P（a）性质”；
②若奇函数y=f（x）具有“P（2）性质”，且f（1）=1，则f（2015）=1；
③若不恒为零的函数y=f（x）同时具有“P（0）性质”和“P（3）性质”，则函数y=f（x）是周期函数；
④若函数y=f（x）具有“P（4）性质”，图象关于点（1，0）成中心对称，且在（-1，0）上单调递减，则y=f（x）在（-2，-1）上单调递减，在（1，2）上单调递增；
其中正确的是①③④（写出所有正确命题的编号）．

1．点P（-2，1）关于直线x+y-3=0对称点的坐标是（2，5）．

18．已知复数z满足（1-i）z=3+5i，则复数z在复平面内对应的点位于（　　）

19．2${\;}^{1-\frac{1}{2}lo{g}_{2}3}$的值等于（　　）

$\frac{2}{3}$$\sqrt{3}$

D．

试题分类