题目内容
【题目】已知点![]() 为圆
为圆![]() 上一点,
上一点,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,点
,点![]() 满足
满足![]() (
(![]() 为坐标原点),点
为坐标原点),点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() ,是否存在定点
,是否存在定点![]() ,使得直线
,使得直线![]() 、
、![]() 的斜率之和恒为0.若存在,则求出点
的斜率之和恒为0.若存在,则求出点![]() 的坐标;若不存在,则请说明理由.
的坐标;若不存在,则请说明理由.
【答案】(Ⅰ)![]() ,(Ⅱ)存在,
,(Ⅱ)存在, ![]()
![]() 或
或![]()
【解析】
(Ⅰ)设![]() ,
,![]() ,由
,由![]() 将
将![]() 用
用![]() 表示,然后将
表示,然后将![]() 代入
代入![]() ,化简即可得到结果;
,化简即可得到结果;
(Ⅱ)假设存在定点![]() 满足题意,设
满足题意,设![]() ,
,![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 的方程为
的方程为![]() ,联立直线与椭圆方程,利用韦达定理和斜率和为0恒成立,可得结果.
,联立直线与椭圆方程,利用韦达定理和斜率和为0恒成立,可得结果.
(Ⅰ)设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
由![]() 得
得![]() ,
,
所以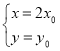 ,所以
,所以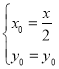 ,
,
又![]() 在圆
在圆![]() 上,
上,
所以![]() ,即
,即![]() .
.
(Ⅱ)假设存在定点![]() 满足题意,设
满足题意,设![]() ,
,![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 的方程为
的方程为![]() ,
,
则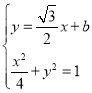 ,得
,得![]() ,,
,,
所以![]()
![]() ,解得
,解得![]()
又![]() ,
,![]() ,
,
因为![]()
![]()
![]() ,
,
所以![]() ,
,
则![]()
![]() ,
,
则![]() ,
,
则![]() ,
,
则![]()
![]()
![]()
![]()
![]()
![]() ,
,
则![]() ,
,
所以![]() 对任意的
对任意的![]() 恒成立,
恒成立,
所以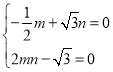 ,解得
,解得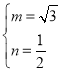 或
或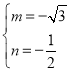 ,
,
所以存在定点![]()
![]() 或
或![]() ,使得
,使得![]() 、
、![]() 的斜率之和恒为0.
的斜率之和恒为0.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
【题目】为了调查某品牌饮料的某种食品添加剂是否超标,现对该品牌下的两种饮料一种是碳酸饮料![]() 含二氧化碳
含二氧化碳![]() ,另一种是果汁饮料
,另一种是果汁饮料![]() 不含二氧化碳
不含二氧化碳![]() 进行检测,现随机抽取了碳酸饮料、果汁饮料各10瓶
进行检测,现随机抽取了碳酸饮料、果汁饮料各10瓶![]() 均是
均是![]() 组成的一个样本,进行了检测,得到了如下茎叶图
组成的一个样本,进行了检测,得到了如下茎叶图![]() 根据国家食品安全规定当该种添加剂的指标大于
根据国家食品安全规定当该种添加剂的指标大于![]() 毫克
毫克![]() 为偏高,反之即为正常.
为偏高,反之即为正常.
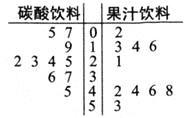
(1)依据上述样本数据,完成下列![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为食品添加剂是否偏高与是否含二氧化碳有关系?
的前提下认为食品添加剂是否偏高与是否含二氧化碳有关系?
正常 | 偏高 | 合计 | |
碳酸饮料 | |||
果汁饮料 | |||
合计 |
(2)现从食品添加剂偏高的样本中随机抽取2瓶饮料去做其它检测,求这两种饮料都被抽到的概率.
参考公式: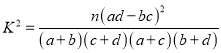 ,其中
,其中![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|