Question

【题目】过点(－1，－2)的直线被圆x2＋y2－2x－2y＋1＝0截得的弦长为，则直线的斜率为________

Answer 1

【答案】1或

【解析】

求出圆心坐标和半径r，由弦长及半径，利用垂径定理及勾股定理求出圆心到直线的距离d ，设出直线的斜率，由直线过（﹣1，﹣2），表示出直线l的方程，利用点到直线的距离公式列出关于k的方程，解出k的值，即为直线l的斜率．

将圆的方程化为标准方程得：（x﹣1）2+（y﹣1）2＝1，∴圆心坐标为（1，1），半径r＝1，

又弦长为，∴圆心到直线的距离，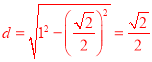

设直线的斜率为k，又直线过（﹣1，﹣2），∴直线的方程为y+2＝k（x+1），即kx﹣y+k﹣2＝0，

∴，即（k﹣1）（7k﹣17）＝0，解得：k＝1或k＝，则直线的斜率为1或．

故答案为1或