题目内容
【题目】已知函数![]() 在
在![]() 处有极值
处有极值![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意得出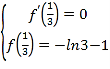 可得出关于
可得出关于![]() 、
、![]() 的方程组,解出这两个量的值,进而可求得函数
的方程组,解出这两个量的值,进而可求得函数![]() 的解析式;
的解析式;
(2)构造函数![]() ,由题意可知,不等式
,由题意可知,不等式![]() 对任意的
对任意的![]() 恒成立,求出导数
恒成立,求出导数![]() ,对实数
,对实数![]() 进行分类讨论,分析函数
进行分类讨论,分析函数![]() 在区间
在区间![]() 上的单调性,求出其最大值
上的单调性,求出其最大值![]() ,通过解不等式
,通过解不等式![]() 可求得实数
可求得实数![]() 的取值范围.
的取值范围.
(1)![]() ,
,![]() ,
,
因为函数![]() 在
在![]() 处有极值
处有极值![]() ,
,
得![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,
,
所以![]() ;
;
(2)不等式![]() 恒成立,
恒成立,
即不等式![]() 恒成立,
恒成立,
令![]() ,
,
则不等式![]() 对任意的
对任意的![]() 恒成立,则
恒成立,则![]() .
.
![]() .
.
又![]() 函数
函数![]() 的定义域为
的定义域为![]() .
.
①当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,则函数
,则函数![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以不等式
,所以不等式![]() 不恒成立;
不恒成立;
②当![]() 时,
时,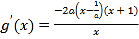 .
.
令![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
故函数![]() 的最大值为
的最大值为![]() ,由题意得需
,由题意得需![]() .
.
令![]() ,
,![]() 函数
函数![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,由
,由![]() ,得
,得![]() ,
,![]() ,
,
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
【题目】为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 | 发病 | 合计 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合计 | 100 | 100 | 200 |
(附: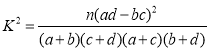 )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
则下列说法正确的:( )
A.至少有99.9%的把握认为“发病与没接种疫苗有关”
B.至多有99%的把握认为“发病与没接种疫苗有关”
C.至多有99.9%的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有0.01%