题目内容
定义在实数集 上的函数
上的函数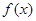 ,如果存在函数
,如果存在函数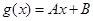 (
( 为常数),使得
为常数),使得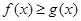 对一切实数
对一切实数 都成立,那么称
都成立,那么称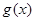 为函数
为函数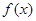 的一个承托函数.给出如下四个结论:
的一个承托函数.给出如下四个结论:
①对于给定的函数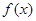 ,其承托函数可能不存在,也可能有无数个;
,其承托函数可能不存在,也可能有无数个;
②定义域和值域都是 的函数
的函数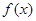 不存在承托函数;
不存在承托函数;
③ 为函数
为函数 的一个承托函数;
的一个承托函数;
④ 为函数
为函数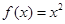 的一个承托函数.
的一个承托函数.
其中所有正确结论的序号是____________________.
 上的函数
上的函数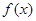 ,如果存在函数
,如果存在函数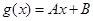 (
( 为常数),使得
为常数),使得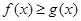 对一切实数
对一切实数 都成立,那么称
都成立,那么称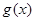 为函数
为函数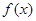 的一个承托函数.给出如下四个结论:
的一个承托函数.给出如下四个结论:①对于给定的函数
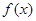 ,其承托函数可能不存在,也可能有无数个;
,其承托函数可能不存在,也可能有无数个;②定义域和值域都是
 的函数
的函数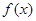 不存在承托函数;
不存在承托函数;③
 为函数
为函数 的一个承托函数;
的一个承托函数;④
 为函数
为函数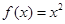 的一个承托函数.
的一个承托函数.其中所有正确结论的序号是____________________.
①③
试题分析:由题意可知,如果存在函数
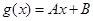 (
(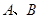 为常数),使得
为常数),使得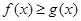 对一切实数
对一切实数 都成立,那么称
都成立,那么称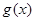 为函数
为函数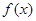 的一个承托函数,那么对于
的一个承托函数,那么对于 来说,不存在承托函数,当
来说,不存在承托函数,当 ,
,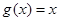 ,则此时有无数个承托函数;②定义域和值域都是
,则此时有无数个承托函数;②定义域和值域都是 的函数
的函数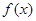 不存在承托函数,因为一个函数本身就是自己的承托函数.故错误;对于③因为
不存在承托函数,因为一个函数本身就是自己的承托函数.故错误;对于③因为
 恒成立,则可知
恒成立,则可知 为函数
为函数 的一个承托函数;成立;对于④如果
的一个承托函数;成立;对于④如果 为函数
为函数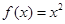 的一个承托函数.则必然有
的一个承托函数.则必然有 并非对任意实数都成立,只有当
并非对任意实数都成立,只有当 或
或 时成立,因此错误;综上可知正确的序号为①③.
时成立,因此错误;综上可知正确的序号为①③.
练习册系列答案
相关题目
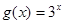 ,
,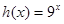 .
.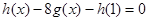 ;
;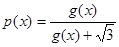 ,求证:
,求证: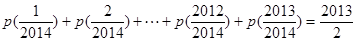 ;
;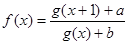 是实数集
是实数集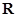 上的奇函数,且
上的奇函数,且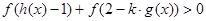 对任意实数
对任意实数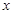 恒成立,求实数
恒成立,求实数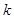 的取值范围.
的取值范围.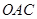 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域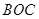 内,乙中转站建在区域
内,乙中转站建在区域 内.分界线
内.分界线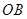 固定,且
固定,且 百米,边界线
百米,边界线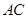 始终过点
始终过点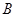 ,边界线
,边界线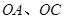 满足
满足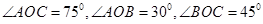 .
.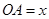 (
(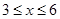 )百米,
)百米,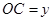 百米.
百米.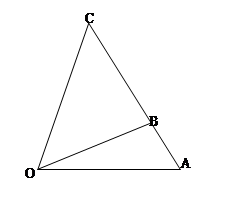
 表示成
表示成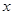 的函数,并求出函数
的函数,并求出函数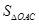 最小,并求出其面积的最小值.
最小,并求出其面积的最小值. 万件与年广告费用
万件与年广告费用 万元满足关系式:
万元满足关系式: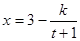 (
( 为常数).若不做广告,则产品的年销售量恰好为1万件.已知2014年生产该产品时,该厂需要先固定投入8万元,并且预计生产每1万件该产品时,需再投入4万元,每件产品的销售价格定为每件产品所需的年平均成本的1.5倍(每件产品的成本包括固定投入和生产再投入两部分,不包括广告促销费用).
为常数).若不做广告,则产品的年销售量恰好为1万件.已知2014年生产该产品时,该厂需要先固定投入8万元,并且预计生产每1万件该产品时,需再投入4万元,每件产品的销售价格定为每件产品所需的年平均成本的1.5倍(每件产品的成本包括固定投入和生产再投入两部分,不包括广告促销费用).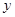 (万元)表示为年广告促销费用
(万元)表示为年广告促销费用 (万元)的函数;
(万元)的函数;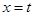 与函数
与函数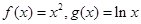 的图像分别交于点
的图像分别交于点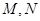 ,则当
,则当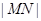 达到最小时
达到最小时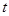 的值为( )
的值为( )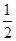
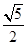
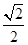
 的递增区间是( )
的递增区间是( )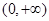


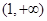
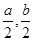 ]
] D,使得f(x)在[
D,使得f(x)在[ )
) )
)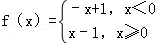 ,则不等式x+(x+1)f(x+1)≤1的解集是( )
,则不等式x+(x+1)f(x+1)≤1的解集是( )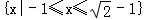
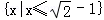
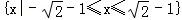
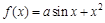 ,若
,若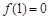 ,则
,则 的值为 .
的值为 .