题目内容
【题目】如图,江的两岸可近似的看成两平行的直线,江岸的一侧有A,B两个蔬菜基地,江的另一侧点C处有一个超市.已知A、B、C中任意两点间的距离为20千米.超市欲在AB之间建一个运输中转站D,A,B两处的蔬菜运抵D处后,再统一经过货轮运抵C处.由于A,B两处蔬菜的差异,这两处的运输费用也不同.如果从A处出发的运输费为每千米2元,从B处出发的运输费为每千米1元,货轮的运输费为每千米3元. 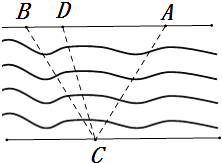
(1)设∠ADC=α,试将运输总费用S(单位:元)表示为α的函数S(α),并写出自变量的取值范围;
(2)问中转站D建在何处时,运输总费用S最小?并求出最小值.
【答案】
(1)解:由题在△ACD中,∵∠CAD=∠ABC=∠ACB= ![]() ,∠CDA=α,∴∠ACD=
,∠CDA=α,∴∠ACD= ![]() ﹣α.
﹣α.
又AB=BC=CA=20,△ACD中,
由正弦定理知 ![]() =
= ![]() =
= ![]() ,得CD=
,得CD= ![]() ,AD=
,AD= ![]() ,
,
∴S=2AD+BD+3CD=AD+3CD+20= ![]() +
+ ![]() +20
+20
=10 ![]()
![]() +20 (
+20 ( ![]() <α<
<α< ![]() )
)
(2)解:S′=10 ![]()
![]() ,令S′=0,得cosα=﹣
,令S′=0,得cosα=﹣ ![]()
当cosα<﹣ ![]() 时,S′<0;当cosα>﹣
时,S′<0;当cosα>﹣ ![]() 时,S′>0,∴当cosα=﹣
时,S′>0,∴当cosα=﹣ ![]() 时S取得最小值.
时S取得最小值.
此时,sinα= ![]() ,AD=10﹣
,AD=10﹣ ![]() ,
,
∴中转站距A处10﹣ ![]() 千米时,运输成本S最小
千米时,运输成本S最小
【解析】(1)由题在△ACD中,由正弦定理求得CD、AD的值,即可求得运输成本S的解析式.(2)利用导数求得cosα=﹣ ![]() 时,函数S取得极小值,由此可得中转点D到A的距离以及S的最小值.
时,函数S取得极小值,由此可得中转点D到A的距离以及S的最小值.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】在某次试验中,两个试验数据x,y的统计结果如下面的表格1所示.
x | 1 | 2 | 3 | 4 | 5 |
y | 2 | 3 | 4 | 4 | 5 |
表格1

(1)在给出的坐标系中画出数据x,y的散点图.
(2)补全表格2,根据表格2中的数据和公式 求下列问题.
求下列问题.
①求出y关于x的回归直线方程![]() 中的
中的![]() .
.
②估计当x=10时,![]() 的值是多少?
的值是多少?
表格2
序号 | x | y | x2 | xy |
1 | 1 | 2 | 1 | 2 |
2 | 2 | 3 | 4 | 6 |
3 | 3 | 4 | 9 | 12 |
4 | 4 | 4 | 16 | 16 |
5 | 5 | 5 | 25 | 25 |
∑ |