题目内容
【题目】已知椭圆![]() 经过点
经过点![]() 离心率为
离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,
两点,![]() 为椭圆
为椭圆![]() 的左焦点,若
的左焦点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() ;
;
(Ⅱ)![]() 或
或![]() .
.
【解析】
(Ⅰ)由题中已知条件可得![]() ,
,![]() ,代入椭圆
,代入椭圆![]() 的方程,将点的坐标代入椭圆方程可求出c的值,进而得出
的方程,将点的坐标代入椭圆方程可求出c的值,进而得出![]() 、b的值,于是可得到椭圆
、b的值,于是可得到椭圆![]() 的方程;
的方程;
(Ⅱ)设直线l的方程为![]() ,设点
,设点![]() ,将直线l的方程代入椭圆
,将直线l的方程代入椭圆![]() 的方程,列出韦达定理,由等式
的方程,列出韦达定理,由等式![]() 结合韦达定理可求出
结合韦达定理可求出![]() 的值,即可求出直线l的方程.
的值,即可求出直线l的方程.
(Ⅰ)设椭圆![]() 的焦距为
的焦距为![]() ,则
,则![]() ,
,
![]() ,
,
所以,椭圆![]() 的方程为
的方程为![]() ,
,
将点![]() 的坐标代入椭圆
的坐标代入椭圆![]() 的方程得
的方程得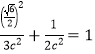 ,
,
解得![]() ,则
,则![]() ,
,
因此,椭圆![]() 的方程为
的方程为![]() ;
;
(Ⅱ)设直线l的方程为![]() ,设点
,设点![]() ,
,
将直线l的方程代入椭圆的方程,并化简得![]() ,
,
![]() ,解得
,解得![]() 或
或![]() .
.
由韦达定理可得![]() ,
,
![]() ,同理可得
,同理可得![]() ,
,
所以,![]()
![]() ,
,
解得![]() ,合乎题意!
,合乎题意!
因此,直线l的方程为![]() 或
或![]() .
.

【题目】如表是某位同学连续5次周考的数学、物理的成绩,结果如下:
周次 | 1 | 2 | 3 | 4 | 5 |
数学( | 79 | 81 | 83 | 85 | 87 |
物理( | 77 | 79 | 79 | 82 | 83 |
参考公式: ,
,![]() ,
,![]() 表示样本均值.
表示样本均值.
(1)求该生5次月考数学成绩的平均分和物理成绩的方差;
(2)一般来说,学生的数学成绩与物理成绩有较强的线性相关关系,根据上表提供的数据,求两个变量![]() 的线性回归方程.
的线性回归方程.
【题目】某校学生会为了解高二年级600名学生课余时间参加中华传统文化活动的情况(每名学生最多参加7场).随机抽取50名学生进行调查,将数据分组整理后,列表如下:
参加场数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
占调查人数的百分比 | 8% | 10% | 20% | 26% | 18% | m% | 4% | 2% |
则以下四个结论中正确的是( )
A.表中m的数值为10
B.估计该年级参加中华传统文化活动场数不高于2场的学生约为108人
C.估计该年级参加中华传统文化活动场数不低于4场的学生约为216人
D.若采用系统抽样方法进行调查,从该校高二600名学生中抽取容量为30的样本,则分段间隔为15