题目内容
【题目】已知椭圆
的方程为
，
，
为椭圆的左右顶点，
为椭圆上不同于.的动点，直线
与直线
，
分别交于
，
两点，若
，则过
，，三点的圆必过
轴上不同于点的定点，其坐标为__________.
【答案】
【解析】
利用椭圆的性质首先证明
，然后结合题意设出直线方程，由点的坐标确定圆的直径所在的位置，最后由直线垂直的充分必要条件可得点D的坐标.
首先证明椭圆的一个性质：
椭圆
，点
是椭圆上关于原点对称的两点，
是椭圆上异于上的一个点，则
.
证明如下：设
，
，
，
由于点
是椭圆上的两点，故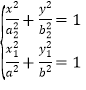
，
两式作差可得：
，
此时
.
故结论成立.
回到本题，由题意可知：
，
设直线PA的方程为：
，则
，
设直线PB的方程为：
，则
，
故
，
故
为外接圆的直径，
设所求的点为
，
则：
，
即
，解得：
，(
舍去).
综上可得：所求点的坐标为：
.
练习册系列答案
相关题目
【题目】2018年12月28日，成雅铁路开通运营，使川西多个市县进入动车时代，融入全国高铁网，这对推动沿线经济社会协调健康发展具有重要意义.在试运行期间，铁道部门计划在成都和雅安两城之间开通高速列车，假设每天7:00-8:00，8:00-9:00两个时间段内各发一趟列车由雅安到成都（两车发车情况互不影响），雅安发车时间及其概率如下表所示：
第一趟列车 | 第二趟列车 | |||||
发车时间 | 7:10 | 7:30 | 7:50 | 8:10 | 8:30 | 8:50 |
概率 | 0.2 | 0.3 | 0.5 | 0.2 | 0.3 | 0.5 |
若小王、小李二人打算乘动车从雅安到成都游玩，假设他们到达雅安火车站候车的时间分别是周六7:00和7:20（只考虑候车时间，不考虑其它因素）.
（1）求小王候车10分钟且小李候车30分钟的概率；
（2）设小李候车所需时间为随机变量
，求的分布列和数学期望
.
