题目内容
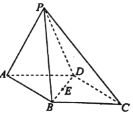
【题目】如图,在三棱锥P—ABC中,PA=3,PB=PC=![]() ,AB=AC=2,BC=
,AB=AC=2,BC=![]() .
.
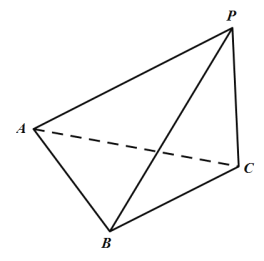
(1)求二面角B—AP—C大小的余弦值;
(2)求点P到底面ABC的距离.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)两三角形![]() 和
和![]() 三边都相等,则两三角形全等,过B向AP边做垂线,过C向AP边做垂线交于点D,那么
三边都相等,则两三角形全等,过B向AP边做垂线,过C向AP边做垂线交于点D,那么![]() 就是要求的二面角,根据已知边长和余弦定理可求出二面角大小的余弦值;(2)取
就是要求的二面角,根据已知边长和余弦定理可求出二面角大小的余弦值;(2)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,在平面
,在平面![]() 中作
中作![]() ,垂足为
,垂足为![]() ,根据直线和平面的位置关系,结合各边的值以及余弦定理和正弦函数可得点P到底面ABC的距离。
,根据直线和平面的位置关系,结合各边的值以及余弦定理和正弦函数可得点P到底面ABC的距离。
解:(1)在![]() 中作
中作![]() ,垂足为
,垂足为![]() ,
,
因为![]() ,
,![]() ,
,![]() 为公共边,所以
为公共边,所以![]() ≌
≌![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角;
的平面角;
又![]() ,所以
,所以![]() ,
,
故![]() 的面积
的面积![]() ,
,
所以![]() ,同理
,同理![]() ,
,
在![]() 中,
中,![]() ,
,
所以,二面角![]() 大小的余弦值为
大小的余弦值为![]() .
.
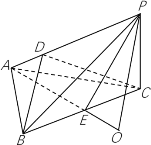
(2)(法一)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,在平面
,在平面![]() 中作
中作![]() ,垂足为
,垂足为![]() .
.
因为![]() ,所以
,所以![]() .同理
.同理![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因此,点![]() 到底面
到底面![]() 的距离即为
的距离即为![]() 的长;
的长;
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
所以,![]() ,
,
在![]() 中,
中,![]() ,
,
综上,点![]() 到底面
到底面![]() 的距离为
的距离为![]() .
.
(法二)由(1)知![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,![]()
所以![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
故![]()
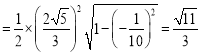 .
.
则![]() .
.
在![]() 中,
中,![]() ,
,![]() ,则
,则![]() .
.
设点![]() 到底面
到底面![]() 的距离为
的距离为![]() ,则
,则![]() ,故
,故![]() .
.

【题目】2018年12月28日,成雅铁路开通运营,使川西多个市县进入动车时代,融入全国高铁网,这对推动沿线经济社会协调健康发展具有重要意义.在试运行期间,铁道部门计划在成都和雅安两城之间开通高速列车,假设每天7:00-8:00,8:00-9:00两个时间段内各发一趟列车由雅安到成都(两车发车情况互不影响),雅安发车时间及其概率如下表所示:
第一趟列车 | 第二趟列车 | |||||
发车时间 | 7:10 | 7:30 | 7:50 | 8:10 | 8:30 | 8:50 |
概率 | 0.2 | 0.3 | 0.5 | 0.2 | 0.3 | 0.5 |
若小王、小李二人打算乘动车从雅安到成都游玩,假设他们到达雅安火车站候车的时间分别是周六7:00和7:20(只考虑候车时间,不考虑其它因素).
(1)求小王候车10分钟且小李候车30分钟的概率;
(2)设小李候车所需时间为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.