题目内容
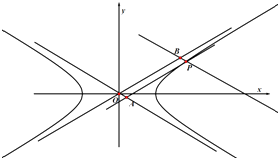
【题目】如图，已知圆
的方程为
，过点
的直线
与圆交于点
，与
轴交于点
，设
，求证：
为定值．
【答案】见解析.
【解析】
先讨论当AB与x轴垂直时，此时点Q与点O重合，从而λ=2，μ=
，λ+μ=
；在讨论AB存在斜率时，：
=.
证明：当AB与x轴垂直时，此时点Q与点O重合，
从而λ=2，μ=，λ+μ=；
当点Q与点O不重合时，直线AB的斜率存在；
设直线AB的方程为y=kx+1，A（x1，y1），B（x2，y2），
则Q（﹣
，0）；
由题设，得x1+=λx1，x2+=μx2，
即λ=1+
，μ=1+
；
所以λ+μ=（1+）+（1+）=2+
；
将y=kx+1代入x2+y2=4，得（1+k2）x2+2kx﹣3=0，
则△＞0，x1+x2=﹣
，x1x2=﹣
，
所以λ+μ=2+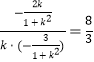
；
综上，λ+μ为定值．
练习册系列答案
相关题目
