题目内容
11.已知Sn是等比数列{an}的前n项和,S3,S9,S6成等差数列,求证:a2,a8,a5成等差数列.分析 由Sn是等比数列{an}的前n项和,且S3,S9,S6成等差数列,利用等差数列的求和公式及等差数列的性质列出关系式,整理后再利用等差数列的性质化简即可得证.
解答 证明:∵Sn是等比数列{an}的前n项和,且S3,S9,S6成等差数列,
∴公比q≠1,且2S9=S3+S6,即2×$\frac{{a}_{1}(1-{q}^{9})}{1-q}$=$\frac{{a}_{1}(1-{q}^{3})}{1-q}$+$\frac{{a}_{1}(1-{q}^{6})}{1-q}$,
整理得:2q9=q3+q6,即2q6=1+q3,
两边同乘以a1q,得2a1q7=a1q+a1q4,即2a8=a2+a5,
则a2,a8,a5成等差数列.
点评 此题考查了等差数列的通项公式,以及等比数列的前n项和公式,熟练掌握公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知集合M是由a=x2-y2,x,y∈N得到所有a值组成的,对于元素6和7,( )
| A. | 仅有7∈M | B. | 仅有6∈M | C. | 都属于M | D. | 都不属于M |
20.已知在(x-2)8的展开式中,x的指数为正偶数的所有项的系数和为( )
| A. | 3281 | B. | -3281 | C. | -3025 | D. | 3025 |
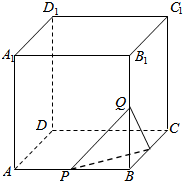 如图所示,P、Q、R分别是正方形的棱AB、BB1、BC的中点,则BD1与平面PQR的位置关系是BD1⊥平面PQR.
如图所示,P、Q、R分别是正方形的棱AB、BB1、BC的中点,则BD1与平面PQR的位置关系是BD1⊥平面PQR.