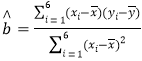题目内容
【题目】为迎接2022年冬奥会，北京市组织中学生开展冰雪运动的培训活动，并在培训结束后对学生进行了考核．记X表示学生的考核成绩，并规定X≥85为考核优秀．为了了解本次培训活动的效果，在参加培训的学生中随机抽取了30名学生的考核成绩，并作成如下茎叶图．
（1）从参加培训的学生中随机选取1人，请根据图中数据，估计这名学生考核优秀的概率；
（2）从图中考核成绩满足X
[70，79]的学生中任取3人，设Y表示这3人重成绩满足
≤10的人数，求Y的分布列和数学期望．
【答案】（1）
（2）
，分布列见解析
【解析】
（1）根据茎叶图得到成绩优秀的人数，然后根据古典概型概率公式求解即可．（2）根据题意先得到
的所有可能取值，然后分别求出对应的概率，进而可得分布列和期望．
（1）设该名学生考核成绩优秀为事件
，由茎叶图中的数据可以知在30名同学的成绩中，优秀的为：85,89,90,90,91,92,93，共有7名同学，
所以
，
所以可估计这名学生考核优秀的概率为．
（2）由题意可得的所有可能取值为
，
因为成绩
的学生共有8人，其中满足
的学生有
人，
所以
，
，
，
．
所以随机变量的分布列为
|
|
|
|
|
|
|
|
|
|
所以
，
即数学期望为
．
智趣寒假作业云南科技出版社系列答案【题目】研究机构对某校学生往返校时间的统计资料表明：该校学生居住地到学校的距离
（单位：千米）和学生花费在上学路上的时间
（单位：分钟）有如下的统计资料：
到学校的距离 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花费的时间 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明与有线性相关关系，试求：
（1）判断与是否有很强的线性相关性？
（相关系数
的绝对值大于0.75时，认为两个变量有很强的线性相关性，精确到0.01）
（2）求线性回归方程
（精确到0.01）；
（3）将
分钟的时间数据
称为美丽数据，现从这6个时间数据中任取2个，求抽取的2个数据全部为美丽数据的概率.
参考数据：
，
，
，
，
，
参考公式：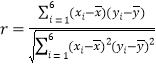
，
