题目内容
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,椭圆
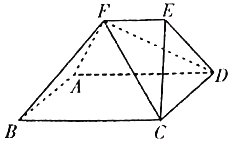
,椭圆![]() 的上、下顶点分别为
的上、下顶点分别为![]() ,
,![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,
,![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() .原点到直线
.原点到直线![]() 的距离为
的距离为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
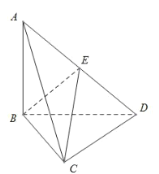
(2)![]() 是椭圆上异于
是椭圆上异于![]() ,
,![]() 的任一点,直线
的任一点,直线![]() ,
,![]() ,分别交
,分别交![]() 轴于点
轴于点![]() ,
,![]() ,若直线
,若直线![]() 与过点
与过点![]() ,
,![]() 的圆
的圆![]() 相切,切点为
相切,切点为![]() ,证明:线段
,证明:线段![]() 的长为定值,并求出该定值.
的长为定值,并求出该定值.
【答案】(1)![]() ; (2)证明见解析;长度为定值2
; (2)证明见解析;长度为定值2
【解析】
(1)根据题意,设![]() ,可得
,可得![]() ,求得
,求得![]() ,结合圆心到直线的距离公式,列出方程,求得
,结合圆心到直线的距离公式,列出方程,求得![]() ,进而求得椭圆的标准方程;
,进而求得椭圆的标准方程;
(2)设![]() ,求得直线
,求得直线![]() 和
和![]() 的方程,分别令
的方程,分别令![]() ,求得
,求得![]() ,得到圆
,得到圆![]() 的圆心坐标,再结合圆的弦长公式和椭圆的方程,即可求解.
的圆心坐标,再结合圆的弦长公式和椭圆的方程,即可求解.
(1)由题意,椭圆![]() :
:![]() 的离心率
的离心率![]() ,即
,即![]()
设![]() ,可得
,可得![]() ,则
,则![]() ,
,
可得![]() ,
,
可得直线![]() 方程为
方程为![]() ,即
,即![]() ,
,
所以原点到直线![]() 的距离为
的距离为![]() ,解得
,解得![]() ,
,
所以![]() ,
,![]() ,椭圆方程为
,椭圆方程为![]() .
.
(2)由(1)可知![]() ,
,![]() ,设
,设![]() ,
,
直线![]() :
:![]() ,令
,令![]() ,得
,得![]() ;
;
直线![]() :
:![]() ,令
,令![]() ,得
,得![]() ;
;
设圆![]() 的圆心为
的圆心为 ,
,
则
 ,
,
 ,
,
所以![]()

![]() ,
,
而![]() ,所以
,所以![]() ,
,
代入可得![]() ,即
,即![]() ,即线段
,即线段![]() 的长度为定值2.
的长度为定值2.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案【题目】为抗击新冠疫情,某企业组织员工进行用款捐物的爱心活动.原则上每人以自愿为基础,捐款不超过400元.现项目负责人统计全体员工数据后,下表为随机抽取的10名员工.的捐款数额.
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
捐款数额 | 124 | 86 | 215 | 53 | 132 | 195 | 400 | 90 | 300 | 225 |
(1)若从这10名员工中任意选取3人,记选到的3人中捐款数额大于200元的人数为X,求X的分布列和数学期望:
(2)以表中选取的10人作为样本.估计该企业全体员工的捐款情况,现从企业员工中依次抽取8人,若抽到k人的捐款数额小于200元的可能性最大,求k的值.
【题目】某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
区间 |
|
|
|
|
|
人数 | 50 | 50 | a | 150 | b |

(1)上表是年龄的频数分布表,求正整数![]() 的值;
的值;
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.