题目内容
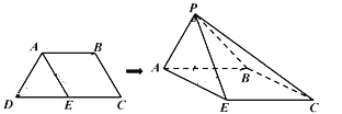
【题目】在四棱锥P-ABCD中，底面ABCD是直角梯形，
，
，平面
平面ABCD.
（1）求证：
；
（2）若
，且
，求四棱锥P-ABCD的体积.
【答案】（1）证明见解析；（2）
【解析】
（1）取CD的中点M，连接AM，由条件知四边形BCMA为正方形，可得
，再由平面
平面ABCD，
平面ABCD，平面
平面
，即可证得
平面PAD，从而证得
；
（2）过点P作
交AD的延长线于点E，可证PE为四棱锥的高，再根据几何关系计算相关棱长，并利用面积公式和
，即可求得
，进而求得四棱锥P-ABCD的体积.
（1）证明：如图，在直角梯形ABCD中，取CD的中点M，连接AM，
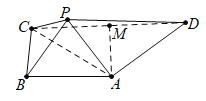
由条件知四边形BCMA为正方形，
，
，
∵平面平面ABCD，平面ABCD，
平面平面，
平面PAD，
平面PAD，
；
（2）过点P作交AD的延长线于点E，如图，
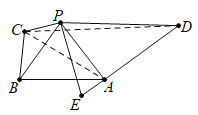
∵平面平面ABCD，
平面PAD，平面平面，
∴
平面ABCD.
设
，则
，
，
，
，
，
，
为等腰三角形，易得
边上的高为
，
，
，
.
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
