Question

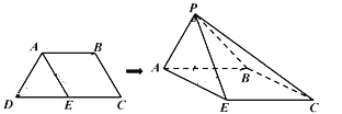
【题目】如图，等腰梯形中，，，，为中点，以为折痕把折起，使点到达点的位置（平面）.

（Ⅰ）证明：；

（Ⅱ）若直线与平面所成的角为，求二面角的余弦值.

Answer 1

【答案】（I）见解析；（II）.

【解析】

（I）先证明，再证明；（II）在平面POB内作PQ⊥OB,垂足为Q，

证明OP⊥平面ABCE，以O为原点，OE为x轴，OB为y轴，OP为z轴，建立空间直角坐标系，利用向量法求二面角的余弦值.

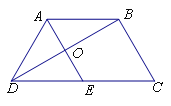
（I）证明：在等腰梯形ABCD中，连接BD，交AE于点O，

∵AB||CE,AB=CE，∴四边形ABCE为平行四边形，∴AE=BC=AD=DE，

∴△ADE为等边三角形，∴在等腰梯形ABCD中，，,

∴在等腰中，

∴,即BD⊥BC，

∴BD⊥AE，

翻折后可得：OP⊥AE,OB⊥AE，又，，

；

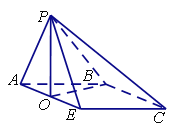
（II）解：在平面POB内作PQ⊥OB,垂足为Q，

因为AE⊥平面POB，∴AE⊥PQ，

因为OB平面ABCE, AE平面ABCE,AE∩OB=O

∴PQ⊥平面ABCE，∴直线PB与平面ABCE夹角为，

又因为OP=OB，∴OP⊥OB，

∴O、Q两点重合，即OP⊥平面ABCE，

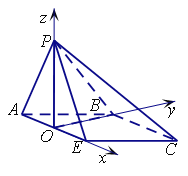
以O为原点，OE为x轴，OB为y轴，OP为z轴，建立空间直角坐标系，由题意得，各点坐标为,

设平面PCE的一个法向量为，

则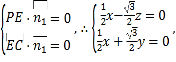

设，则y=-1,z=1，

∴，

由题意得平面PAE的一个法向量，

设二面角A-EP-C为，.

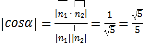易知二面角A-EP-C为钝角，所以.