题目内容
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | 当1≤x≤20时,m=20+ |
当21≤x≤30时,m=10+ |
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
【答案】
(1)
解:分两种情况
①当1≤x≤20时,将m=25代入m=20+ ![]() x,解得x=10.
x,解得x=10.
②当21≤x≤30时,25=10+ ![]() ,解得x=28.
,解得x=28.
经检验x=28是方程的解.
∴x=28.
答:第10天或第28天时该商品为25元/件.
(2)
解:分两种情况
①当1≤x≤20时,y=(m﹣10)n=(20+ ![]() x﹣10)(50﹣x)=﹣
x﹣10)(50﹣x)=﹣ ![]() x2+15x+500,
x2+15x+500,
②当21≤x≤30时,y=(10+ ![]() ﹣10)(50﹣x)=
﹣10)(50﹣x)= ![]() -420
-420
综上所述: 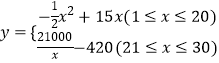
(3)
解:①当1≤x≤20时
由y=﹣ ![]() x2+15x+500=﹣
x2+15x+500=﹣ ![]() (x﹣15)2+
(x﹣15)2+ ![]() ,
,
∵a=﹣ ![]() <0,
<0,
∴当x=15时,y最大值= ![]() ,
,
②当21≤x≤30时
由y= ![]() ﹣420,可知y随x的增大而减小
﹣420,可知y随x的增大而减小
∴当x=21时,y最大值= ![]() ﹣420=580元
﹣420=580元
∵ ![]()
∴第15天时获得利润最大,最大利润为612.5元.
【解析】本题考查二次函数的应用、反比例函数的性质等知识,解题的关键是学会构建函数,利用二次函数的性质解决问题,属于中考常考题型.
(1)分两种情形分别代入解方程即可;
(2)分两种情形写出所获利润y(元)关于x(天)的函数关系式即可;
(3)分两种情形根据函数的性质解决问题即可.

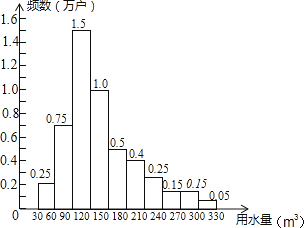
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.