题目内容
【题目】以直角坐标系的原点
为极点， 
轴正半轴为极轴，并在两种坐标系中取相同的长度单位，已知直线
的参数方程为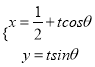
，（ 
为参数， 
），曲线
的极坐标方程为
.
（1）求曲线
的直角坐标方程；
（2）设直线
与曲线
相交于
， 
两点，当
变化时，求
的最小值.
【答案】（1）
（2）2
【解析】试题分析：（1）本问考查极坐标与直角坐标互化公式，根据
可得
，所以曲线C的直角坐标方程为
；（2）本问考查直线参数方程标准形式下的几何意义，即将直线参数方程的标准形式
，代入到曲线C的直角坐标方程，得到关于t的一元二次方程，设
两点对应的参数分别为
，列出
， 
， 
，于是可以求出
的最小值.
试题解析：（I）由
由，得
曲线 
的直角坐标方程为
（II）将直线
的参数方程代入，得
设
两点对应的参数分别为
则
， 
，
当
时， 
的最小值为2.
练习册系列答案
小学课时特训系列答案
相关题目
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品，利用30天的时间销售一种成本为10元/件的商品售后，经过统计得到此商品单价在第x天（x为正整数）销售的相关信息，如表所示：
销售量n（件） | n=50﹣x |
销售单价m（元/件） | 当1≤x≤20时，m=20+ |
当21≤x≤30时，m=10+ |
（1）请计算第几天该商品单价为25元/件？
（2）求网店销售该商品30天里所获利润y（元）关于x（天）的函数关系式；
（3）这30天中第几天获得的利润最大？最大利润是多少？
