题目内容
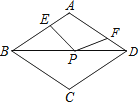
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,侧面
的正方形,侧面![]()
底面![]() ,且
,且![]() ,
, ![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:面![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?说明理由.
?说明理由.
【答案】(1)详见解析;(2)详见解析;(3)线段![]() 上存在点
上存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() .
.
【解析】试题分析:(Ⅰ)连接AC,则F是AC的中点,E为PC 的中点,证明EF∥PA,留言在线与平面平行的判定定理证明EF∥平面PAD;
(Ⅱ)先证明CD⊥PA,然后证明PA⊥PD.利用直线与平面垂直的判定定理证明PA⊥平面PCD,最后根据面面垂直的判定定理即可得到面PAB⊥面PDC.
(Ⅲ)假设在线段AB上,存在点G,使得二面角C-PD-G的余弦值为![]() ,然后以O为原点,直线OA,OF,OP分别为x,y,z轴建立空间直角坐标系,设G(1,a,0)(0≤a≤2).利用空间向量的坐标运算求出a值,即可得出结论.
,然后以O为原点,直线OA,OF,OP分别为x,y,z轴建立空间直角坐标系,设G(1,a,0)(0≤a≤2).利用空间向量的坐标运算求出a值,即可得出结论.
试题解析:
(Ⅰ)证明:连结AC,由已知,F为AC的中点, ![]() 为
为![]() 中点.∴在
中点.∴在![]() 中,
中, ![]() //
// ![]()
且![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ∴
∴![]()
(Ⅱ)证明:因为平面![]() 平面
平面![]() , 平面
, 平面![]() 面
面![]()
![]() 为正方形,
为正方形, ![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
∴![]()
又![]() ,所以
,所以![]() 是等腰直角三角形, 且
是等腰直角三角形, 且![]() ,即
,即![]() .
.
![]() ,且
,且![]() 、
、![]() 面
面![]()
![]() 面
面![]()
又![]() 面
面![]() , ∴面
, ∴面![]() 面
面![]()
(Ⅲ)如图,
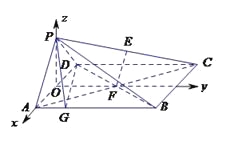
取![]() 的中点
的中点![]() ,连结
,连结![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() .
.
∵侧面![]() 底面
底面![]() ,
,
![]() ,
,
∴![]() ,
,
而![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() ,又
,又![]() 是正方形,故
是正方形,故![]() .
.
∵![]() ,∴
,∴![]() ,
, ![]() .
.
以![]() 为原点,直线
为原点,直线![]() 分别为
分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则有![]() ,
, ![]() ,
, ![]() .
.
若在![]() 上存在点
上存在点![]() 使得二面角
使得二面角![]() 的余弦值为
的余弦值为![]() ,连结
,连结![]()
设![]() .
.
由(Ⅱ)知平面![]() 的法向量为
的法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() .∵
.∵![]() ,
,
∴由![]() 可得
可得![]() ,令
,令![]() ,则
,则![]() ,
,
故![]() ∴
∴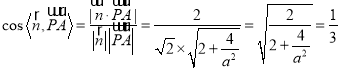 ,解得,
,解得, ![]() . 所以在线段
. 所以在线段![]() 上存在点
上存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,此时
,此时![]() .
.

【题目】某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
南靖 | 厦门 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)参加活动的教师有人,学生有人;
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.
①求y关于x的函数关系式;
②若购买一、二等座票全部费用不多于1032元,则提早前往的教师最多只能多少人?
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | 当1≤x≤20时,m=20+ |
当21≤x≤30时,m=10+ |
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?