题目内容
【题目】已知函数![]() ,若对于区间
,若对于区间![]() 上的任意
上的任意![]() ,都有
,都有![]() ,则实数
,则实数![]() 的最小值是( )
的最小值是( )
A. 20B. 18
C. 3D. 0
【答案】A
【解析】
对于区间[﹣3,2]上的任意x1,x2都有|f(x1)﹣f(x2)|≤t,等价于对于区间[﹣3,2]上
的任意x,都有f(x)max﹣f(x)min≤t,利用导数确定函数的单调性,求最值,即可得出
结论.
对于区间[﹣3,2]上的任意x1,x2都有|f(x1)﹣f(x2)|≤t,
等价于对于区间[﹣3,2]上的任意x,都有f(x)max﹣f(x)min≤t,
∵f(x)=x3﹣3x﹣1,∴f′(x)=3x2﹣3=3(x﹣1)(x+1),
∵x∈[﹣3,2],
∴函数在[﹣3,﹣1]、[1,2]上单调递增,在[﹣1,1]上单调递减,
∴f(x)max=f(2)=f(﹣1)=1,f(x)min=f(﹣3)=﹣19,
∴f(x)max﹣f(x)min=20,
∴t≥20,
∴实数t的最小值是20,
故答案为:A

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
喜欢 | 不喜欢 | 合计 | |
大于40岁 | 20 | 5 | 25 |
20岁至40岁 | 10 | 20 | 30 |
合计 | 30 | 25 | 55 |
(1)判断是否有![]() 的把握认为喜欢“人文景观”景点与年龄有关?
的把握认为喜欢“人文景观”景点与年龄有关?
(2)已知20岁到40岁喜欢“人文景观”景点的市民中,有3位还比较喜欢“自然景观”景点,现在从20岁到40岁的10位市民中,选出3名,记选出喜欢“自然景观”景点的人数为![]() ,求
,求![]() 的分布列、数学期望.
的分布列、数学期望.
(参考公式:![]() ,其中
,其中![]() )
)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】2018年10月28日,重庆公交车坠江事件震惊全国,也引发了广大群众的思考——如何做一个文明的乘客.全国各地大部分社区组织居民学习了文明乘车规范.![]() 社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
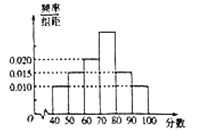
(1)求得分在![]() 上的频率;
上的频率;
(2)求![]() 社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
(3)由于部分居民认为此项学习不具有必要性,![]() 社区委员会对社区居民的学习态度作调查,所得结果统计如下:(表中数据单位:人)
社区委员会对社区居民的学习态度作调查,所得结果统计如下:(表中数据单位:人)
认为此项学习十分必要 | 认为此项学习不必要 | |
50岁以上 | 400 | 600 |
50岁及50岁以下 | 800 | 200 |
根据上述数据,计算是否有![]() 的把握认为居民的学习态度与年龄相关.
的把握认为居民的学习态度与年龄相关.
附:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |