题目内容
19.已知等差数列{an}的首项al=1,公差d>0,且{an}的第二项、第五项、第十四项成等比数列.(1)求数列{an}的通项公式;
(2)设${b_n}=\frac{1}{{n({a_n}+5)}}(n∈{N^*})$,记Sn为数列{bn}的前n项和,求Sn并说明是否存在最大的整数t,使得对任意的n均有${S_n}>\frac{t}{36}$总成立?若存在,求出t;若不存在,请说明理由.
分析 (1)由{an}的第二项、第五项、第十四项成等比数列,可得$({a}_{1}+4d)^{2}$=(a1+d)(a1+13d),化简整理即可得出.
(2)${b_n}=\frac{1}{{n({a_n}+5)}}(n∈{N^*})$,bn=$\frac{1}{n(2n+4)}$=$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+2})$.利用“裂项求和”、“放缩法”、不等式的性质即可得出.
解答 解:(1)∵{an}的第二项、第五项、第十四项成等比数列,
∴$({a}_{1}+4d)^{2}$=(a1+d)(a1+13d),整理得2a1d=d2,
∴2d=d2,∵d>0,∴d=2.
∴an=1+2(n-1)=2n-1.
(2)${b_n}=\frac{1}{{n({a_n}+5)}}(n∈{N^*})$,
∴bn=$\frac{1}{n(2n+4)}$=$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+2})$.
∴Sn=$\frac{1}{4}[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{n-1}-\frac{1}{n+1})$+$(\frac{1}{n}-\frac{1}{n+2})]$
=$\frac{1}{4}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$≥$\frac{1}{4}(\frac{3}{2}-\frac{1}{2}-\frac{1}{3})$=$\frac{1}{6}$.
假设存在最大的整数t,使得对任意的n均有${S_n}>\frac{t}{36}$总成立,
则$\frac{t}{36}<\frac{1}{6}$,解得t<6.
∴适合不等式的最大整数为5.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“裂项求和”、“放缩法”、不等式的性质,考查了推理能力与计算能力,属于中档题.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案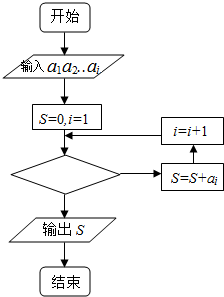 某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表所示:
某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表所示:| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数ai | 9 | 13 | 11 | 7 | 5 | 6 |
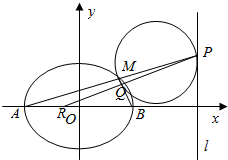 如图,AB是长轴长为6,焦距为2的椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,直线l的方程为x=9,M是椭圆C上异于A,B的一点,直线AM交l于点P.
如图,AB是长轴长为6,焦距为2的椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,直线l的方程为x=9,M是椭圆C上异于A,B的一点,直线AM交l于点P.