题目内容
9.已知圆C:x2+(y-1)2=5,直线l:mx-y+1-m=0.(1)求证:对m∈R,直线l与圆C总有两个不同的交点.
(2)若定点P(1,1)分弦AB为$\frac{AP}{PB}$=$\frac{1}{2}$,求此直线l 的方程.
(3)求弦AB中点M的轨迹方程.
分析 (1)将直线l的方程变形提出m,根据直线方程的斜截式,求出直线恒过点(1,1),将(1,1)代入圆方程的左边,判断出点在圆内部,得证.
(2)作出辅助线,利用圆的弦割线定理求出PA的长,求出A的坐标,又直线过(1,0)点,利用直线方程的两点式写出直线的方程.
(3)将直线l的方程与圆的方程联立,利用韦达定理得到两个交点坐标的和,利用中点坐标公式求出AB的中点,消去m得到弦AB的中点M的轨迹方程.
解答 (1)证明:∵直线L:mx-y+1-m=0即为y=m(x-1)+1
∴直线l恒过(1,1)
∵12+(1-1)2=1<5
∴(1,1)在圆C:x2+(y-1)2=5的内部
综上,对任意的m∈R,直线L与圆C一定有两个不同的交点
(2)解:∵直线l:mx-y+1-m=0,y-1=m(x-1),
∴直线l过定点(1,1).
作平行于x轴,且过圆心(0,1)的直线,交圆于MN两点,显然,PM=$\sqrt{5}$-1,PN=$\sqrt{5}$+1,
由弦割线定理,PA•PB=PA•2PA=2PA2=PM•PN=4
∴PA2=2.
∵PA2=(x-1)2+(y-1)2=2,
又因为A点在圆上,A点坐标满足圆方程x2+(y-1)2=5,
联立方程组,解得,x=2,
代入解得,y=0或2,
∴A(2,0)或A(2,2).
由两点确定直线,得,y-1=$\frac{0-1}{2-1}$•(x-1)=-(x-1),得y+x-2=0直线一条;
y-1=$\frac{2-1}{2-1}$•(x-1)=x-1,得,y=x另一条直线.
∴此时L的方程为x-y=0或x+y-2=0
(3)解:圆C:x2+(y-1)2=5 ①
直线l:mx-y+1-m=0②
联立①②得(1+m2)x2-2m2x+m2-5=0
设A(x1,y1),B(x2,y2),则
x1+x2=$\frac{2{m}^{2}}{1+{m}^{2}}$,y1+y2=$\frac{2({m}^{2}-m+1)}{1+{m}^{2}}$
设弦AB的中点M为(x,y)则有x=$\frac{{m}^{2}}{1+{m}^{2}}$,y=$\frac{{m}^{2}-m+1}{1+{m}^{2}}$
则y=1-$\frac{m}{1+{m}^{2}}$,
∴$\frac{m}{1+{m}^{2}}$=1-y,$\frac{m}{1+{m}^{2}}$=x两式相除得,m=$\frac{x}{1-y}$
代入第一式即消去m得到x2+y2-x-2y+1=0
故弦AB的中点M的轨迹方程为x2+y2-x-2y+1=0 (x≠1)
点评 判断直线与圆的位置关系,一般利用圆心与直线的距离与半径的大小关系加以判断,有时也可转化为直线恒过的点圆圆的位置关系;解决直线与圆的相交的弦的中点问题,一般将直线与圆的方程联立,利用韦达定理.

| A. | (0,+∞) | B. | (-∞,0] | C. | (-∞,0) | D. | (-∞,+∞) |
| A. | $\frac{1}{a}$+$\frac{1}{b}$=1 | B. | a2+b2=1 | C. | $\frac{1}{a^2}$+$\frac{1}{b^2}$=1 | D. | a+b=ab |
| A. | 1.75万件 | B. | 1.7万件 | C. | 2万件 | D. | 1.8万件 |
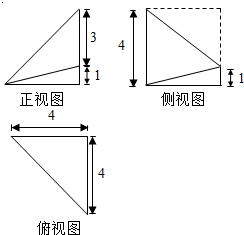 已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于$\frac{40}{3}$.
已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于$\frac{40}{3}$.