题目内容
设数列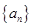 的前
的前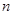 项和
项和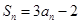
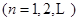 .
.
(1)证明数列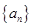 是等比数列;
是等比数列;
(2)若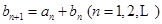 ,且
,且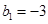 ,求数列
,求数列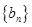 的前
的前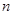 项和
项和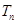 .
.
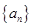 的前
的前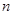 项和
项和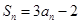
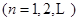 .
.(1)证明数列
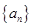 是等比数列;
是等比数列;(2)若
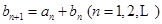 ,且
,且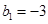 ,求数列
,求数列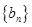 的前
的前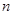 项和
项和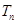 .
.(Ⅰ)由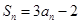
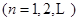 ,及
,及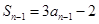
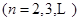 ,
,
相减得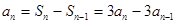 ,即
,即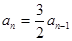 .
.
验证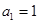 .适合,得到结论,
.适合,得到结论,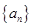 是首项为
是首项为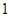 ,公比是
,公比是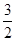 的等比数列.
的等比数列.
(Ⅱ)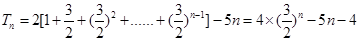 .
.
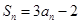
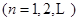 ,及
,及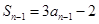
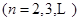 ,
,相减得
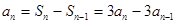 ,即
,即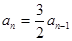 .
.验证
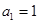 .适合,得到结论,
.适合,得到结论,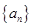 是首项为
是首项为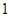 ,公比是
,公比是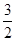 的等比数列.
的等比数列.(Ⅱ)
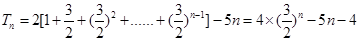 .
.试题分析:(Ⅰ)证:因为
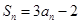
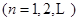 ,
,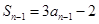
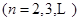 ,
,所以当
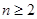 时,
时,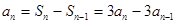 ,整理得
,整理得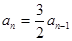 .
.由
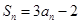 ,令
,令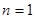 ,得
,得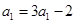 ,解得
,解得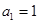 .
.所以
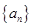 是首项为
是首项为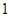 ,公比是
,公比是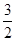 的等比数列.
的等比数列.(Ⅱ)解:由
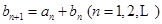 ,得
,得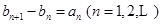 .
.所以
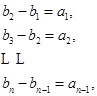
从而
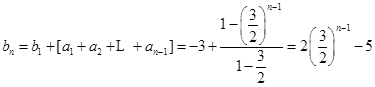 .
.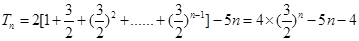 .
.点评:中档题,本题通过确定
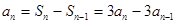 ,达到证明数列是等比数列的目的。根据
,达到证明数列是等比数列的目的。根据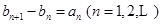 受到启发,利用“累加法”求得
受到启发,利用“累加法”求得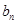 ,进一步利用“分组求和法”确定得到
,进一步利用“分组求和法”确定得到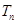 。“裂项相消法”“错位相减法”也常常考到的数列求和方法。
。“裂项相消法”“错位相减法”也常常考到的数列求和方法。
练习册系列答案
相关题目
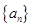 中公比
中公比 ,
, ,则公比q= .
,则公比q= .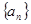 中,已知
中,已知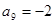 ,则此数列前17项之积为( )
,则此数列前17项之积为( )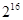
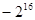
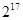
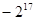
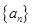 的前
的前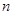 项和
项和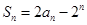 。
。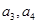 ;
;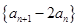 是等比数列;
是等比数列;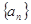 中,
中,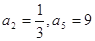 ,则
,则 。
。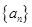 中,
中,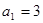 ,公比
,公比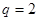 ,从第
,从第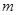 项到第
项到第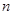 项的和为360(
项的和为360(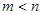 ),
),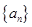 中,首项
中,首项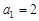 ,前3项和为14,则
,前3项和为14,则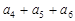 值为_____________.
值为_____________.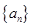 中,若
中,若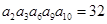 ,则
,则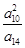 的值为
的值为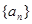 满足:
满足: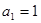 ,
,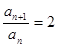 ,数列
,数列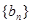 满足:
满足: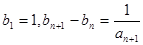 ,(以上
,(以上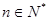 ),则
),则