题目内容
各项都是正数的等比数列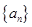 中,首项
中,首项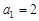 ,前3项和为14,则
,前3项和为14,则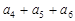 值为_____________.
值为_____________.
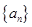 中,首项
中,首项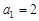 ,前3项和为14,则
,前3项和为14,则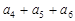 值为_____________.
值为_____________.112;
试题分析:根据题意,由于各项都是正数的等比数列
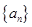 中,首项
中,首项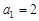 ,前3项和为14,则根据等长连续片段的和构成的数列依然是等比数列,且公比为
,前3项和为14,则根据等长连续片段的和构成的数列依然是等比数列,且公比为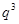 ,那么结合已知
,那么结合已知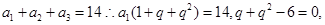 ,那么可知
,那么可知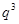 =8,故可知
=8,故可知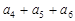 =14
=14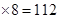 ,故答案为112.
,故答案为112.点评:解决的关键是对于等比数列的公式以及性质的灵活运用,属于基础题。

练习册系列答案
相关题目
 中,
中, ,公比
,公比 .
. 为
为
 ,求数列
,求数列 的通项公式.
的通项公式.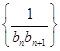 的前n项和Sn=________.
的前n项和Sn=________.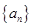 的前
的前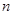 项和
项和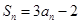
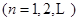 .
.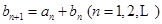 ,且
,且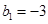 ,求数列
,求数列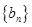 的前
的前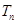 .
.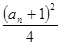
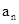 }满足
}满足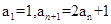 。
。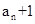 }是等比数列。
}是等比数列。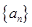 的各项均为正数,且
的各项均为正数,且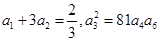
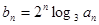 求数列
求数列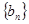 的前
的前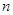 项和
项和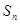 .
.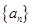 是首项为
是首项为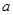 且公比q不等于1的等比数列,
且公比q不等于1的等比数列,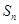 是其前n项的和,
是其前n项的和,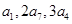 成等差数列.证明:
成等差数列.证明: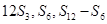 成等比数列.
成等比数列.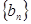 中,若
中,若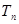 是数列
是数列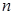 项积,则有
项积,则有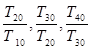 也成等比数列,且公比为
也成等比数列,且公比为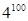 ;类比上述结论,相应的在公差为3的等差数列
;类比上述结论,相应的在公差为3的等差数列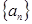 中,若
中,若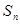 是
是