题目内容
设数列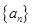 的前
的前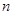 项和
项和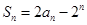 。
。
(1)求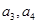 ;
;
(2)证明: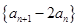 是等比数列;
是等比数列;
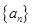 的前
的前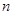 项和
项和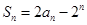 。
。(1)求
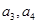 ;
;(2)证明:
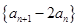 是等比数列;
是等比数列;(1)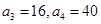 (2)先构造
(2)先构造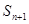 ,作差得到递推式化简从而证明.
,作差得到递推式化简从而证明.
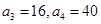 (2)先构造
(2)先构造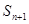 ,作差得到递推式化简从而证明.
,作差得到递推式化简从而证明.试题分析:(1)
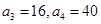
(2)由题设
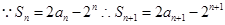
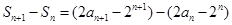
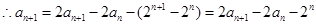
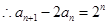
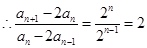
所以
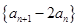 是首项为2,公比为2的等比数列
是首项为2,公比为2的等比数列点评:本题的关键是利用当
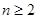 时,
时,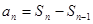 间的关系,消掉
间的关系,消掉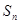 从而得到递推公式.
从而得到递推公式.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
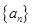 的前
的前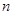 项和
项和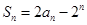 。
。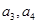 ;
;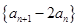 是等比数列;
是等比数列;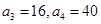 (2)先构造
(2)先构造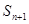 ,作差得到递推式化简从而证明.
,作差得到递推式化简从而证明.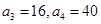
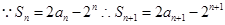
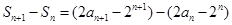
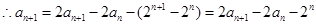
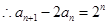
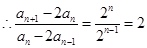
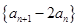 是首项为2,公比为2的等比数列
是首项为2,公比为2的等比数列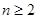 时,
时,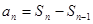 间的关系,消掉
间的关系,消掉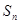 从而得到递推公式.
从而得到递推公式.
 名校课堂系列答案
名校课堂系列答案