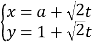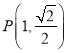题目内容
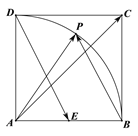
【题目】如图，在边长为1的正方形ABCD中，E为AB的中点，P为以A为圆心，AB为半径的圆弧（在正方形内，包括边界点）上的任意一点，则
的取值范围是________； 若向量
，则
的最小值为_________.
【答案】 
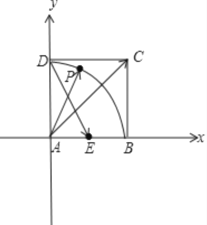
【解析】分析：首先根据图形的特征，建立适当的平面直角坐标系，根据正方形的边长，设出点P的坐标，利用终点坐标减去起点坐标，得到对应向量的坐标利用向量数量积坐标公式求得结果；再者就是利用向量相等得到坐标的关系，将其值转化为对应自变量的函数关系，结合自变量的取值范围，求得最小值.
详解：如图，以A为原点，以AB所在直线为x轴，建立平面直角坐标系，结合题意，可知
，所以
，因为
，所以
，所以
，所以
的范围是；
根据
，可得
，即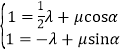
，从而可以求得
，
所以
，
因为
，所以
，所以当
取得最大值1时，同时
取得最小值0，这时
取得最小值为
，所以的最小值是.
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案【题目】关于函数
,有下列结论:
①
的定义域为(-1, 1); ②的值域为(
, 
);
③的图象关于原点成中心对称; ④在其定义域上是减函数;
⑤对的定义城中任意
都有
.
其中正确的结论序号为__________.
【题目】某企业为打入国际市场，决定从
，
两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表：（单位：万美元）
项目类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| 20 |
| 10 | 200 |
| 40 | 8 | 18 | 120 |
其中年固定成本与年生产的件数无关，
为待定常数，其值由生产产品的原材料价格决定，预计
.另外，年销售
件产品时需上交
万美元的特别关税.假设生产出来的产品都能在当年销售出去.
（1）写出该厂分别投资生产，两种产品的年利润
、
与生产相应产品的件数之间的函数关系，并指明其定义域；
（2）如何投资才可获得最大年利润？请你做出规划.
