题目内容
【题目】如果函数![]() 的定义域为
的定义域为![]() ,对于定义域内的任意
,对于定义域内的任意![]() 存在实数
存在实数![]() 使得
使得![]() 成立,则称此函数具有“
成立,则称此函数具有“![]() 性质”.
性质”.
(1)判断函数![]() 是否具有“
是否具有“![]() 性质”,若具有“
性质”,若具有“![]() 性质”,写出所有
性质”,写出所有![]() 的值;若不具有“
的值;若不具有“![]() 性质”,请说明理由.
性质”,请说明理由.
(2)设函数![]() 具有“
具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,求当
,求当![]() 时函数
时函数![]() 的解析式;若
的解析式;若![]() 与
与![]()
![]() 交点个数为1001个,求
交点个数为1001个,求![]() 的值.
的值.
【答案】(1)![]() ,理由见解析(2)
,理由见解析(2)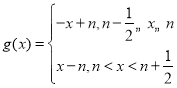 ,
,![]() ;
;![]() .
.
【解析】
(1)根据题意先检验![]() 是否成立即可检验
是否成立即可检验![]() 是否具有“
是否具有“![]() (a)性质(2)由题意可得
(a)性质(2)由题意可得![]() ,
,![]() ,据此递推关系可推断函数
,据此递推关系可推断函数![]() 的周期,根据交点周期性出现的规律即可求解满足条件的
的周期,根据交点周期性出现的规律即可求解满足条件的![]() ,以及
,以及![]() 的解析式.
的解析式.
(1)由![]() 得
得![]() ,
,
根据诱导公式得![]() .
.
![]() 具有“
具有“![]() (a)性质”,其中
(a)性质”,其中![]() .
.
(2)![]() 具有“
具有“![]() 性质”,
性质”,
![]() ,
,![]() ,
,
![]() ,
,
从而得到![]() 是以2为周期的函数.
是以2为周期的函数.
又![]() ,则
,则![]() ,
,
![]() .
.
再设![]() ,
,
当![]() ,则
,则![]() ,则
,则![]() ,
,
![]() ;
;
当![]() ,则
,则![]() ,则
,则![]()
![]() ;
;
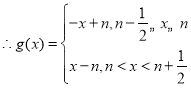 ,
,![]() ;.
;.
![]() 对于
对于![]() ,
,![]() ,都有
,都有![]() ,而
,而![]() ,
,
![]() ,
,
![]() 是周期为1的函数.
是周期为1的函数.
①当![]() 时,要使
时,要使![]() 与
与![]() 有1001个交点,只要
有1001个交点,只要![]() 与
与![]() 在
在![]() ,
,![]() 有1000个交点,而在
有1000个交点,而在![]() ,
,![]() 有一个交点.
有一个交点.
![]() 过
过![]() ,
,![]() ,从而得
,从而得![]()
②当![]() 时,同理可得
时,同理可得![]()
③当![]() 时,不合题意.
时,不合题意.
综上所述![]()

练习册系列答案
相关题目
【题目】设直线系M:xcosθ+(y﹣2)sinθ=1(0≤θ≤2π),对于下列四个命题:
A.M中所有直线均经过一个定点 |
B.存在定点P不在M中的任一条直线上 |
C.对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上 |
D.M中的直线所能围成的正三角形面积都相等 |
其中真命题的代号是 (写出所有真命题的代号).