题目内容
某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙,地面利用原地面均不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,屋顶每平方米造价20元.
(1)仓库面积 的最大允许值是多少?
的最大允许值是多少?
(2)为使面积 达到最大而实际投入又不超过预算,正面铁栅应设计为多长?
达到最大而实际投入又不超过预算,正面铁栅应设计为多长?
(1)100平分米;(2)15米
解析试题分析:(1)设铁栅长 米,侧墙宽
米,侧墙宽 米,
米,
则由题意得: , 3分
, 3分
即 ① (以上两处的“
① (以上两处的“ ”号写成“
”号写成“ ”号不扣分)
”号不扣分)
由于 ②,
②,
由①②可得 ,
, ,
,
所以 的最大允许值为100平分米. 8分
的最大允许值为100平分米. 8分
(2)由(1)得当面积 达到最大而实际投入又不超过预算时,
达到最大而实际投入又不超过预算时,
有: 且
且 ,从而
,从而 .
.
即正面铁栅应设计为15米长. 12分
考点:函数的实际应用;基本不等式。
点评:面对实际问题,能够迅速的建立数学模型是一种重要的基本技能。比如此题,在读题时把题目中提供的“条件”逐条的翻译成“数学语言”,这个过程就是数学建模的过程。做此题的关键就是列出不等式。

练习册系列答案
相关题目
 ,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.
,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.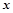 (单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当
(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当 时,车流速度v是车流密度
时,车流速度v是车流密度 时,求函数
时,求函数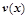 的表达式;
的表达式; 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时) 的二次项系数为
的二次项系数为 ,满足不等式
,满足不等式 的解集为(1,3),且方程
的解集为(1,3),且方程 有两个相等的实根,求
有两个相等的实根,求 个单位的固体碱在水中逐渐溶化,水中的碱浓度
个单位的固体碱在水中逐渐溶化,水中的碱浓度 与时间
与时间 (小时)的关系可近似地表示为:
(小时)的关系可近似地表示为: ,只有当污染河道水中碱的浓度不低于
,只有当污染河道水中碱的浓度不低于 时,才能对污染产生有效的抑制作用.
时,才能对污染产生有效的抑制作用. ,求
,求 是奇函数,
是奇函数, 是偶函数。
是偶函数。 的值;
的值; 若
若 对任意
对任意 恒成立,求实数
恒成立,求实数 %,则销售量将减少
%,则销售量将减少 %,且该化工产品每吨的价格上涨幅度不超过
%,且该化工产品每吨的价格上涨幅度不超过 %,
%, 其中
其中 为正常数
为正常数

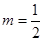 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大? ,及函数
,及函数 。
。 的不等式
的不等式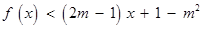 的解集为
的解集为 ,其中
,其中 为正常数。
为正常数。 的值;
的值; R
R 如何取值时,函数
如何取值时,函数

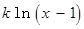 存在极值点,并求出极值点;
存在极值点,并求出极值点; ,且
,且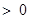 ,求证:
,求证:
 。
。