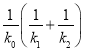题目内容
【题目】已知椭圆C:![]() (
(![]() )的短轴长为
)的短轴长为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的标准方程;
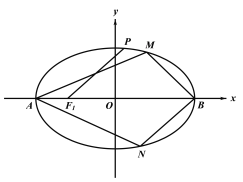
(2)设M,N分别为椭圆C的左、右顶点,过点![]() 且不与x轴重合的直线
且不与x轴重合的直线![]() 与椭圆C相交于A,B两点是否存在实数t(
与椭圆C相交于A,B两点是否存在实数t(![]() ),使得直线
),使得直线![]() :
:![]() 与直线
与直线![]() 的交点P满足P,A,M三点共线?若存在,求出
的交点P满足P,A,M三点共线?若存在,求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]()
(2)存在,直线![]() :
:![]()
【解析】
(1)利用椭圆的几何性质建立方程组求解即可;
(2)假设存在满足题意的直线![]() ,先设出
,先设出![]() 的方程
的方程![]() ,设出
,设出![]() ,
,![]() 、
、![]() ,
,![]() ,联立方程组得出根与系数关系,然后求出
,联立方程组得出根与系数关系,然后求出![]() 点坐标,利用三点共线建立方程,将根与系数关系代入整理、化简、求解即可.
点坐标,利用三点共线建立方程,将根与系数关系代入整理、化简、求解即可.
解:(1)由于短轴长为![]() ,所以
,所以![]() ,
,![]() .
.
又离心率![]() ,且
,且![]() ,解得
,解得![]() .
.
所以椭圆C的标准方程为![]() .
.
(2)假设存在直线![]() 满足条件,设
满足条件,设![]() 的方程为
的方程为![]() ,且
,且![]() ,
,![]() .
.
联立方程组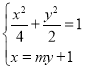 ,消去x可得
,消去x可得![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
由于![]() ,
,![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
则![]() :
:![]() (
(![]() )与直线
)与直线![]() 的交点P的坐标为
的交点P的坐标为![]() ,且
,且![]() ,
,![]() .
.
当![]() ,
,![]() ,
,![]() 三点共线时有
三点共线时有![]() 与
与![]() 共线.
共线.
所以![]() ,即
,即![]() .
.
由于![]() ,所以
,所以![]() ,
,
所以![]() ,解得
,解得![]() ,所以存在直线
,所以存在直线![]() :
:![]() 满足条件.
满足条件.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加 班级工作 | 不太主动参加 班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法能否有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系?并说明理由.(参考下表)
P(K2 ≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: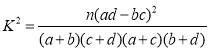 ,其中
,其中![]() )
)
【题目】![]() 大学就业部从该大学2018年已就业的大学本科毕业生中随机抽取了100人进行月薪情况的问卷调查,经统计发现,他们的月薪收入在3000元到10000元之间,具体统计数据如表:
大学就业部从该大学2018年已就业的大学本科毕业生中随机抽取了100人进行月薪情况的问卷调查,经统计发现,他们的月薪收入在3000元到10000元之间,具体统计数据如表:
月薪(百万) |
|
|
|
|
|
|
|
人数 | 2 | 15 | 20 | 15 | 24 | 10 | 4 |
(1)经统计发现,该大学2018届的大学本科毕业生月薪![]() (单位:百元)近似地服从正态分布
(单位:百元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值).若
(每组数据取区间的中点值).若![]() 落在区间
落在区间![]() 的左侧,则可认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,为以后的毕业生就业提供更好的指导意见.现该校2018届大学本科毕业生张茗的月薪为3600元,试判断张茗是否属于“就业不理想”的学生;
的左侧,则可认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,为以后的毕业生就业提供更好的指导意见.现该校2018届大学本科毕业生张茗的月薪为3600元,试判断张茗是否属于“就业不理想”的学生;
(2)①将样本的频率视为总体的概率,若![]() 大学领导决定从
大学领导决定从![]() 大学2018届所有本毕业生中任意选取5人前去探访,记这5人中月薪不低于8000元的人数为
大学2018届所有本毕业生中任意选取5人前去探访,记这5人中月薪不低于8000元的人数为![]() ,求
,求![]() 的数学期望与方差;
的数学期望与方差;
②在(1)的条件下,中国移动赞助了![]() 大学的这次社会调查活动,并为这次参与调查的大学本科毕业生制定了赠送话费的活动,赠送方式为:月薪低于
大学的这次社会调查活动,并为这次参与调查的大学本科毕业生制定了赠送话费的活动,赠送方式为:月薪低于![]() 的获赠两次随机话费,月薪不低于
的获赠两次随机话费,月薪不低于![]() 的获赠一次随机话费;每次赠送的话费及对应的概率分别为:
的获赠一次随机话费;每次赠送的话费及对应的概率分别为:
赠送话费(单位:元) | 50 | 100 | 150 |
概率 |
|
|
|
则张茗预期获得的话费为多少元?(结果保留整数)