题目内容
19.已知函数f(x)=y=$\left\{\begin{array}{l}{{x}^{2}-2x,x∈[-2,-1)}\\{-{x}^{2}+2x,x∈[-1,3)}\end{array}\right.$,求f(x)的值域.分析 根据二次函数的单调性及取得顶点情况与比较端点值来求原函数在每一段里的f(x)的范围,这两段函数下求得的f(x)的范围再求并集即可得出原函数f(x)的值域.
解答 解:①x∈[-2,-1)时,f(x)=x2-2x=(x-1)2-1;
f(x)在[-2,-1)上单调递减;
∴f(-1)<f(x)≤f(-2);
∴3<f(x)≤8;
②x∈[-1,3)时,f(x)=-x2+2x=-(x-1)2+1;
f(-1)=f(3)=-3,f(1)=1;
∴-3≤f(x)≤1;
∴综上得,函数f(x)的值域为[-3,1]∪(3,8].
点评 考查函数值域的概念,分段函数值域的求法:在每一段上求函数的范围,然后求并集,以及二次函数值域的求法.

练习册系列答案
相关题目
8.已知集合A={x|x2-10x+16<0},B={x|0<x<6},则A∩B=( )
| A. | {x|0<x<2} | B. | {x|2<x<6} | C. | {x|6<x<8} |
9.已知f(x)为R上的增函数,则满足f($\frac{1}{x}$)<f(1)的实数x的取值范围是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,0)∪(0,1) | D. | (-∞,0)∪(1,+∞) |
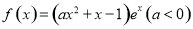 .
.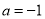 时,函数
时,函数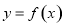 与
与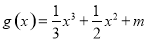 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数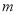 的范围;
的范围;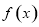 的单调性.
的单调性. ,则
,则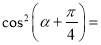 ____________.
____________.