题目内容
【题目】设 
，若0≤a≤1，n∈N＋且n≥2，求证：f(2x)≥2f(x).
【答案】见解析
【解析】试题分析：本题主要考查了一般形式的柯西不等式，本题的解答是利用分析法，解决问题的关键是将
f(2x)＞2f(x)转化为
，然后再根据对数函数 单调性进一步化简，搭配成柯西不等式形式，证明即可.
试题解析：∵
，
∴要证f(2x)≥2f(x)，
只要证
，
即证
(*)
也即证n[12x＋22x＋…＋(n－1)2x＋a·n2x]
≥[1x＋2x＋…＋(n－1)x＋a·nx]2 ，
∵0≤a≤1，∴a＞a2 ， 根据柯西不等式得
n[12x＋22x＋…＋(n－1)2x＋a·n2x]
，
≥[1x＋2x＋…＋(n－1)x＋a·nx]2 ，
即(*)式显然成立，故原不等式成立.
练习册系列答案
相关题目
【题目】为了丰富退休生活，老王坚持每天健步走，并用计步器记录每天健步走的步数.他从某月中随机抽取20天的健步走步数（老王每天健步走的步数都在
之间，单位：千步），绘制出频率分布直方图（不完整）如图所示.
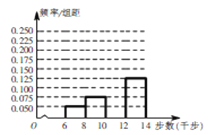
（1）完成频率分布直方图，并估计该月老王每天健步走的平均步数(每组数据可用区间中点值代替；
（2）某健康组织对健步走步数的评价标准如下表:
每天步数分组(千步) |
|
|
|
评价级别 | 及格 | 良好 | 优秀 |
现从这20天中评价级别是“及格”或“良好”的天数里随机抽取2天，求这2天的健步走结果属于同一评价级别的概率.
