题目内容
【题目】在平面直角坐标系中,O为坐标原点,A、B、C三点满足 ![]() =
= ![]() +
+ ![]()
![]() .
.
(1)求证:A、B、C三点共线;
(2)求 ![]() 的值;
的值;
(3)已知A(1,cosx)、B(1+cosx,cosx),x∈[0, ![]() ],f(x)=
],f(x)= ![]()
![]() ﹣(2m+
﹣(2m+ ![]() )|
)| ![]() |的最小值为﹣
|的最小值为﹣ ![]() ,求实数m的值.
,求实数m的值.
【答案】
(1)证明:由已知 ![]() ,即
,即 ![]() ,
,
∴ ![]() ∥
∥ ![]() .又∵
.又∵ ![]() 、
、 ![]() 有公共点A,∴A,B,C三点共线.
有公共点A,∴A,B,C三点共线.
(2)解:∵ ![]() ,∴
,∴ ![]()
![]() =
= ![]()
![]() ∴
∴ ![]() ,∴
,∴ 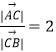 .
.
(3)解:∵C为 ![]() 的定比分点,λ=2,∴
的定比分点,λ=2,∴ ![]() ,
, ![]()
∴ ![]()
![]()
∵ ![]() ,∴cosx∈[0,1]
,∴cosx∈[0,1]
当m<0时,当cosx=0时,f(x)取最小值1与已知相矛盾;
当0≤m≤1时,当cosx=m时,f(x)取最小值1﹣m2,得 ![]() (舍)
(舍)
当m>1时,当cosx=1时,f(x)取得最小值2﹣2m,得 ![]()
综上所述, ![]() 为所求
为所求
【解析】(1)求证:A、B、C三点共线,可证由三点组成的两个向量共线,由题设条件不难得到;(2)由(1) ![]() 变形即可得到两向量模的比值;(3)求出
变形即可得到两向量模的比值;(3)求出 ![]() 的解析式,判断其最值取到的位置,令其最小值为-
的解析式,判断其最值取到的位置,令其最小值为- ![]() ,由参数即可,
,由参数即可,
【考点精析】认真审题,首先需要了解三角函数的最值(函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某单位![]() 名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组
名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
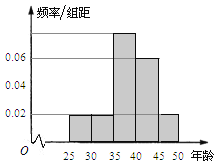
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(I)现要从年龄低于40岁的员工中用分层抽样的方法抽取12人,则年龄在第![]() 组的员工人数分别是多少?
组的员工人数分别是多少?
(II)为了交流读书心得,现从上述![]() 人中再随机抽取
人中再随机抽取![]() 人发言,设
人发言,设![]() 人中年龄在
人中年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(III)为了估计该单位员工的阅读倾向,现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查,调查结果如下表所示:(单位:人)
喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
男 | 14 | 4 | 18 |
女 | 8 | 14 | 22 |
合计 | 22 | 18 | 40 |
根据表中数据,我们能否有![]() 的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
附:![]() ,其中
,其中![]()
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |