题目内容
20.解方程:(1gx)2-1gx2一3=0.分析 利用方程求出lgx,然后求解即可.
解答 解:(1gx)2-1gx2-3=0.
可得(1gx)2-21gx-3=0,
解得lgx=-1,或者lgx=3,
解得x=$\frac{1}{10}$或x=1000,
经检验可知x=$\frac{1}{10}$或x=1000是方程的解.
点评 本题考查函数的零点与方程的根的关系,考查计算能力.

练习册系列答案
相关题目
10.已知等比数列{an}首项为1,公比q=2,前n项和为Sn,则下列结论正确的是( )
| A. | ?n∈N*,Sn<an+1 | |
| B. | ?n∈N*,an•an+1≤an+2 | |
| C. | ?n0∈N*,a${\;}_{{n}_{0}}$+a${\;}_{{n}_{0}+2}$=2a${\;}_{{n}_{0}+1}$ | |
| D. | ?n0∈N*,a${\;}_{{n}_{0}}$+a${\;}_{{n}_{0}+3}$=a${\;}_{{n}_{0}+1}$+a${\;}_{{n}_{0}+2}$ |
9.下表是某市近30年来月平均气温(℃)的数据统计表:则适合这组数据的函数模型是( )
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 平均温度 | -5.9 | -3.3 | 3.3 | 9.3 | 15.1 | 20.3 | 22.8 | 22.2 | 18.2 | 11.9 | 4.3 | -2.4 |
| A. | y=acos$\frac{πx}{6}$ | B. | y=acos$\frac{(x-1)π}{6}$+k(a>0,k>0) | ||
| C. | y=-acos$\frac{(x-1)π}{6}$+k(a>0,k>0) | D. | y=acos$\frac{πx}{6}$-3 |
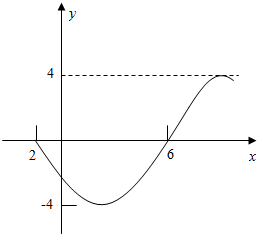 函数f(x)=Asin(ωx+φ)(ω>0,|φ|<π,x∈R)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(ω>0,|φ|<π,x∈R)的部分图象如图所示.