题目内容
12.已知:空间四边形ABCD的各条边和对角线长都等于a,E,F,G分别是AB,CD,AD的中点.(1)给出直线EG和直线FG的一个方向向量;
(2)给出平面CDE的一个法向量.
分析 (1)由三角形中位线定理得EG∥BD,FG∥CA,从而得到$\overrightarrow{BD}$是直线EG的一个方向向量,$\overrightarrow{AC}$是直线FG的一个方向向量.
(2)由已知得到CE⊥AB,DE⊥AB,从而AB⊥平面CDE,由此得到平面CDE的一个法向量为$\overrightarrow{AB}$
解答 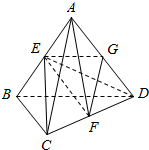 解:(1)∵空间四边形ABCD的各条边和对角线长都等于a,
解:(1)∵空间四边形ABCD的各条边和对角线长都等于a,
E,F,G分别是AB,CD,AD的中点,
∴EG∥BD,FG∥CA,
∴$\overrightarrow{BD}$是直线EG的一个方向向量,$\overrightarrow{AC}$是直线FG的一个方向向量.
(2)∵空间四边形ABCD的各条边和对角线长都等于a,E是AB的中点,
∴CE⊥AB,DE⊥AB,
∵CE∩DE=E,∴AB⊥平面CDE,
∴平面CDE的一个法向量为$\overrightarrow{AB}$.
点评 本题考查直线的方向向量的求法,才副标题平面的法向量的求法,是基础题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
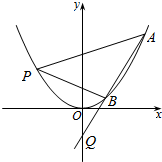 已知抛物线C:x2=4y的焦点为F,O为坐标原点,过Q(0,m)作直线交抛物线C于A,B两点,点P在抛物线C上,且满足$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FP}$=$\overrightarrow{0}$.
已知抛物线C:x2=4y的焦点为F,O为坐标原点,过Q(0,m)作直线交抛物线C于A,B两点,点P在抛物线C上,且满足$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FP}$=$\overrightarrow{0}$.