题目内容
已知函数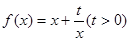 和点
和点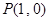 ,过点
,过点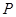 作曲线
作曲线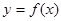 的两条切线
的两条切线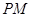 、
、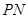 ,切点分别为
,切点分别为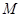 、
、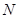 .
.
(Ⅰ)设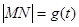 ,试求函数
,试求函数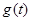 的表达式;
的表达式;
(Ⅱ)是否存在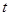 ,使得
,使得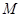 、
、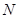 与
与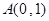 三点共线.若存在,求出
三点共线.若存在,求出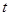 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数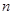 ,在区间
,在区间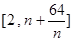 内总存在
内总存在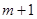 个实数
个实数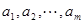 ,
,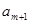 ,使得不等式
,使得不等式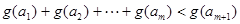 成立,求
成立,求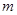 的最大值.
的最大值.
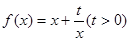 和点
和点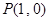 ,过点
,过点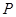 作曲线
作曲线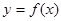 的两条切线
的两条切线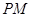 、
、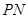 ,切点分别为
,切点分别为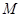 、
、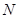 .
.(Ⅰ)设
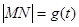 ,试求函数
,试求函数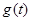 的表达式;
的表达式;(Ⅱ)是否存在
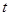 ,使得
,使得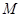 、
、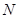 与
与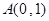 三点共线.若存在,求出
三点共线.若存在,求出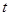 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数
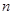 ,在区间
,在区间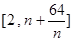 内总存在
内总存在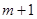 个实数
个实数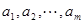 ,
,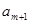 ,使得不等式
,使得不等式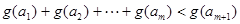 成立,求
成立,求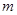 的最大值.
的最大值.(Ⅰ)函数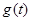 的表达式为
的表达式为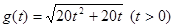 .
.
(Ⅱ)存在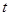 ,使得点
,使得点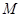 、
、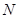 与
与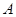 三点共线,且
三点共线,且 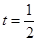 .
.
(Ⅲ)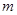 的最大值为
的最大值为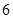 .
.
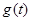 的表达式为
的表达式为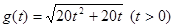 .
.(Ⅱ)存在
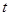 ,使得点
,使得点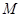 、
、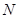 与
与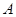 三点共线,且
三点共线,且 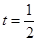 .
.(Ⅲ)
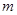 的最大值为
的最大值为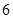 .
.试题分析:(Ⅰ)设
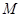 、
、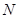 两点的横坐标分别为
两点的横坐标分别为 、
、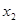 ,
, 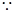
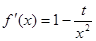 ,
,∴切线
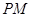 的方程为:
的方程为: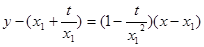 ,
,又
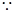 切线
切线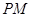 过点
过点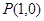 ,
, 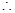 有
有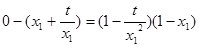 ,即
,即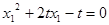 , (1)
, (1)同理,由切线
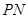 也过点
也过点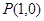 ,得
,得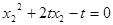 .(2)
.(2)由(1)、(2),可得
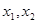 是方程
是方程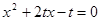 的两根,
的两根,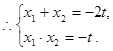 ( * )
( * )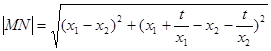
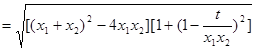 ,
,把( * )式代入,得
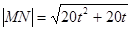 ,
,因此,函数
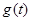 的表达式为
的表达式为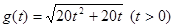 .
.(Ⅱ)当点
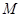 、
、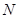 与
与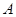 共线时,
共线时,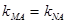 ,
,
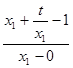 =
=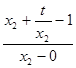 ,即
,即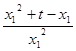 =
=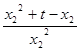 ,
,化简,得
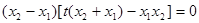 ,
,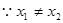 ,
,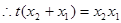 . (3)
. (3)把(*)式代入(3),解得
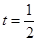 .
. 存在
存在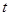 ,使得点
,使得点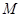 、
、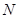 与
与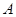 三点共线,且
三点共线,且 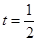 .
.(Ⅲ)解法
 :易知
:易知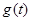 在区间
在区间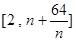 上为增函数,
上为增函数,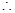
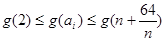
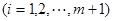 ,
,则
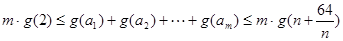 .
.依题意,不等式
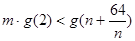 对一切的正整数
对一切的正整数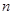 恒成立,
恒成立,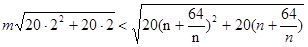 ,
,即
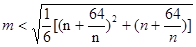 对一切的正整数
对一切的正整数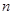 恒成立.
恒成立.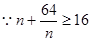 ,
, 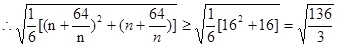 ,
,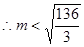 .
.由于
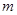 为正整数,
为正整数,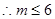 .
.又当
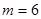 时,存在
时,存在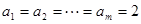 ,
,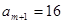 ,对所有的
,对所有的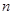 满足条件.
满足条件.因此,
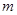 的最大值为
的最大值为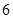 .
.解法
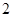 :依题意,当区间
:依题意,当区间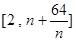 的长度最小时,
的长度最小时,得到的
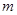 最大值,即是所求值.
最大值,即是所求值.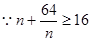 ,
,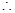 长度最小的区间为
长度最小的区间为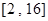
当
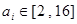
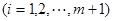 时,与解法
时,与解法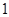 相同分析,得
相同分析,得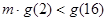 ,
,解得
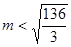 . 后面解题步骤与解法
. 后面解题步骤与解法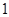 相同(略).
相同(略).点评:难题,切线的斜率等于函数在切点的导函数值。不等式恒成立问题,常常转化成求函数的最值问题。(III)小题,通过构造函数,研究函数的单调性、极值(最值),进一步确定得到参数的范围。

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
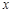 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为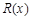 万元,且
万元,且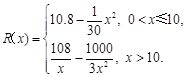
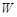 (万元)关于年产量
(万元)关于年产量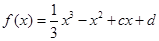
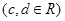 ,其图象为曲线
,其图象为曲线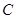 ,点
,点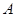 为曲线
为曲线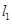 与曲线
与曲线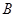 ,在点
,在点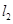 .
.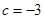 时,求函数
时,求函数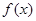 的单调区间;
的单调区间;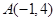 时,
时,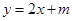 ,求实数
,求实数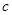 和
和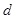 的值;
的值;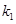 、
、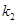 ,试问:是否存在常数
,试问:是否存在常数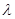 ,使得
,使得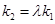 ?若存在,求出
?若存在,求出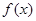 与
与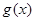 和区间D,如果存在
和区间D,如果存在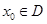 ,使
,使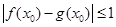 ,则称
,则称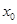 是函数
是函数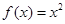 ,
, ②
②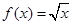 ,
,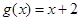
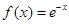 ,
,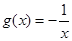 ④
④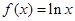 ,
,
 上存在“友好点”的有( )
上存在“友好点”的有( )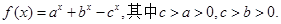
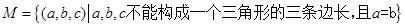 ,则
,则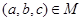 所对应的
所对应的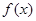 的零点的取值集合为 .
的零点的取值集合为 .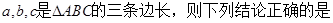 ______.(写出所有正确结论的序号)
______.(写出所有正确结论的序号)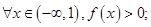
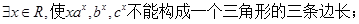
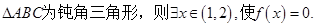
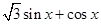
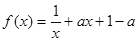 ,
,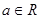 ,
,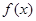 为奇函数,求
为奇函数,求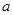 的值;
的值;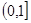 上是减函数;
上是减函数;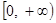 上的最小值.
上的最小值. 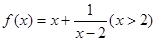 在
在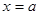 处取最小值, 则
处取最小值, 则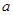 =( )
=( )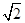
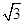
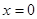 是函数
是函数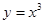 的极值点;
的极值点;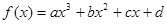 有极值点的充要条件是
有极值点的充要条件是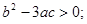
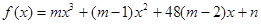 在区间
在区间 上单调递减.
上单调递减.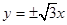 ,则其离心率为2.
,则其离心率为2.