题目内容
【题目】如图，平面直角坐标系中，射线y=x（x≥0）和y=0（x≥0）上分别依次有点A1、A2 ， …，An ， …，和点B1 ， B2 ， …，Bn…，其中 
， 
， 
．且 
， 
（n=2，3，4…）．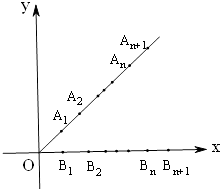 
（1）用n表示|OAn|及点An的坐标；
（2）用n表示|BnBn+1|及点Bn的坐标；
（3）写出四边形AnAn+1Bn+1Bn的面积关于n的表达式S（n），并求S（n）的最大值．
【答案】
（1）解：∵ 
∴ 
（2）解： 
，
∴ 
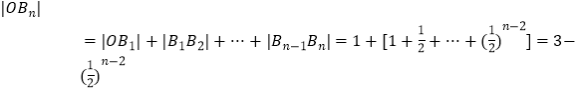（3）解： 
，
∴ 
∵ 
，
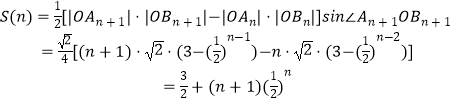
∴n≥4时，S（n）单调递减．
又 
， 
．
∴n=2或3时，S（n）取得最大值 
【解析】（1）由 ，能求出 ．（2）由 ，知 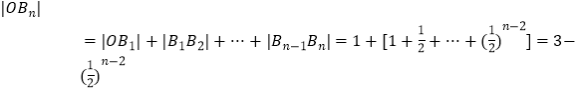，由此能用n表示|BnBn+1|及点Bn的坐标．（3）由 ，写出四边形AnAn+1Bn+1Bn的面积关于n的表达式S（n），并求出S（n）的最大值．
【考点精析】本题主要考查了数列的通项公式的相关知识点，需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．
练习册系列答案
相关题目
【题目】某校举行环保知识竞赛，为了了解本次竞赛成绩情况，从得分不低于50分的试卷中随机抽取100名学生的成绩（得分均为正数，满分100分），进行统计，请根据频率分布表中所提供的数据，解答下列问题：
（Ⅰ）求a、b的值；
（Ⅱ）若从成绩较好的第3、4、5组中，按分层抽样的方法抽取6人参加社区志愿者活动，并从中选出2人做负责人，求2人中至少有1人是第四组的概率．
组号 | 分组 | 频数 | 频率 |
第1组 | [50，60] | 5 | 0.05 |
第2组 | [60，70] | a | 0.35 |
第3组 | [70，80] | 30 | b |
第4组 | [80，90] | 20 | 0.20 |
第5组 | [90，100] | 10 | 0.10 |
合计 | 100 | 1.00 | |
