题目内容
已知正方形ABCD的边长为1,分别取边BC、CD的中点E、F,连接AE、EF、AF,以AE、EF、FA为折痕,折叠使点B、C、D重合于一点P.(1)求证:AP⊥EF;
(2)求证:平面APE⊥平面APF;
(3)求异面直线PA和EF的距离.
【答案】分析:(1)这是一个“折叠问题”,需抓住不变的线线垂直关系、长度关系.比如:∠APE=∠APF=90°,PE∩PF=P,所以PA⊥平面PEF.
又因为EF?平面PEF,所以PA⊥EF.
(2)由长度关系易得:∠EPF=90°,且∠APE=90°,AP∩PF=P,所以PE⊥平面APF.又PE?平面PAE,所以平面APE⊥平面APF.
(3)求异面直线的距离是立体几何的一个难点,其主要原因是公垂线段较难找,本题可以采用“线面距离法”:即选择异面直线中的一条,过它作另一条直线的平行平面,则此直线与平面的距离即为所求异面直线间的距离.在面PEF中,作PG⊥EF,垂足为G,
则PG是AP与EF的公垂线.在等腰Rt△PEF中,进一步可以求得PG的长度.
解答: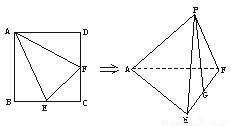 (1)证明:如图,∵∠APE=∠APF=90°,
(1)证明:如图,∵∠APE=∠APF=90°,
PE∩PF=P,∴PA⊥平面PEF.
∵EF?平面PEF,∴PA⊥EF.
(2)证明:∵∠APE=∠EPF=90°,
AP∩PF=P,∴PE⊥平面APF.又PE?平面PAE,
∴平面APE⊥平面APF.
(3)解:在面PEF中,作PG⊥EF,垂足为G,
∵AP与面PEF垂直,PG?平面PEF,
∴AP⊥PG,PG⊥EF,PG是AP与EF的公垂线.
在等腰Rt△PEF中,PE=PF= ,∠EPF=90°,∴PG=EG=
,∠EPF=90°,∴PG=EG=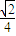 .
.
点评:本小题考查空间中的线面关系及面面关系,异面直线的距离、解三角形等基础知识考查空间想象能力和思维能力.
又因为EF?平面PEF,所以PA⊥EF.
(2)由长度关系易得:∠EPF=90°,且∠APE=90°,AP∩PF=P,所以PE⊥平面APF.又PE?平面PAE,所以平面APE⊥平面APF.
(3)求异面直线的距离是立体几何的一个难点,其主要原因是公垂线段较难找,本题可以采用“线面距离法”:即选择异面直线中的一条,过它作另一条直线的平行平面,则此直线与平面的距离即为所求异面直线间的距离.在面PEF中,作PG⊥EF,垂足为G,
则PG是AP与EF的公垂线.在等腰Rt△PEF中,进一步可以求得PG的长度.
解答:
 (1)证明:如图,∵∠APE=∠APF=90°,
(1)证明:如图,∵∠APE=∠APF=90°,PE∩PF=P,∴PA⊥平面PEF.
∵EF?平面PEF,∴PA⊥EF.
(2)证明:∵∠APE=∠EPF=90°,
AP∩PF=P,∴PE⊥平面APF.又PE?平面PAE,
∴平面APE⊥平面APF.
(3)解:在面PEF中,作PG⊥EF,垂足为G,
∵AP与面PEF垂直,PG?平面PEF,
∴AP⊥PG,PG⊥EF,PG是AP与EF的公垂线.
在等腰Rt△PEF中,PE=PF=
 ,∠EPF=90°,∴PG=EG=
,∠EPF=90°,∴PG=EG=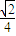 .
.点评:本小题考查空间中的线面关系及面面关系,异面直线的距离、解三角形等基础知识考查空间想象能力和思维能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知正方形ABCD的边长为1,设
=
,
=
,
=
,则|
-
+
|等于( )
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
B、
| ||
| C、2 | ||
D、2
|
 已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1,
已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1, 如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.
如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.