题目内容
15.设△ABC的内角A,B,C的对边分别为a,b,c,且S△ABC=bccosA.(1)求tan2A的值;
(2)若b2=a2+c2-$\sqrt{2}$ac,b=$\sqrt{5}$,求c.
分析 (1)由题意和三角形的面积公式求出tanA的值,由二倍角的正切公式求出tan2A的值;
(2)由题意和余弦定理求出cosB,由内角的范围和特殊角的余弦值求出B,由同角三角函数的基本关系求出sinA,由正弦定理求出边a,代入b2=a2+c2-$\sqrt{2}$ac求出c的值.
解答 解:(1)由题意知,S△ABC=bccosA,
则$\frac{1}{2}$bcsinA=bccosA,则sinA=2cosA,即tanA=2,
所以tan2A=$\frac{2tanA}{1-ta{n}^{2}A}$=$\frac{4}{1-4}$=-$\frac{4}{3}$;
(2)因为b2=a2+c2-$\sqrt{2}$ac,所以a2+c2-b2=$\sqrt{2}$ac,
由余弦定理得,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{\sqrt{2}}{2}$,
由0<B<π得,B=$\frac{π}{4}$,
由(1)知tanA=2,则$\left\{\begin{array}{l}{sinA=2cosA}\\{si{n}^{2}A+co{s}^{2}A=1}\end{array}\right.$,
解得sinA=±$\frac{2\sqrt{5}}{5}$,
因为sinA>0,所以sinA=$\frac{2\sqrt{5}}{5}$,
由正弦定理得,$\frac{b}{sinB}=\frac{a}{sinA}$,a=$\frac{bsinA}{sinB}$=$\frac{\sqrt{5}×\frac{2\sqrt{5}}{5}}{\frac{\sqrt{2}}{2}}$=2$\sqrt{2}$,
代入b2=a2+c2-$\sqrt{2}$ac得,5=8+c2-4c,则c2-4c+3=0,
解得c=3或1.
点评 本题考查正弦、余弦定理,同角三角函数的基本关系,三角形的面积公式,二倍角的正切公式等,考查公式较多,但难度不大,注意内角的范围.

| A. | f(x)=-x2+3x-1 | B. | f(x)=-x2-$\frac{3}{2}$x-1 | C. | f(x)=$\frac{1}{2}$x2-$\frac{3}{2}$x+2 | D. | f(x)=2x2-$\frac{1}{2}$x+2 |
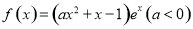 .
.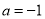 时,函数
时,函数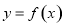 与
与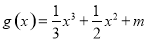 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数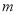 的范围;
的范围;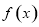 的单调性.
的单调性.