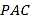题目内容
【题目】如图,在直三棱柱ABCA1B1C1中,AB=AC=![]() ,BC=AA1=2,O,M分别为BC,AA1的中点.
,BC=AA1=2,O,M分别为BC,AA1的中点.
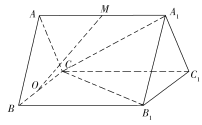
(1)求证:OM∥平面CB1A1;
(2)求点M到平面CB1A1的距离.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连接BC1,交CB1于点N,则N为CB1的中点,连接ON,可得ON∥BB1,再结合ON=MA1,可得四边形ONA1M为平行四边形,则有OM∥NA1,再由线面平行的判定可证得OM∥平面CB1A1;
(2)由OM∥平面CB1A1,可知点M到平面CB1A1的距离等于点O到平面CB1A1的距离,然后利用等积法可求解.
(1)如图,连接BC1,交CB1于点N,连接A1N,ON.
则N为CB1的中点,
又∵O为BC的中点,
∴ON∥BB1,且ON=![]() BB1,
BB1,
又∵M为AA1的中点,
∴MA1∥BB1,且MA1=![]() BB1,
BB1,
∴ON∥MA1且ON=MA1,
∴四边形ONA1M为平行四边形,
∴OM∥NA1,
又∵NA1平面CB1A1,OM平面CB1A1,
∴OM∥平面CB1A1.
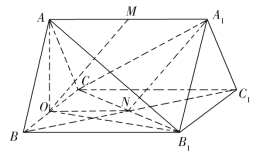
(2)如图,连接AO,OB1,AB1.
∵AB=AC,O为BC的中点,∴AO⊥BC,
又∵直三棱柱ABCA1B1C1中,平面CBB1C1⊥平面ABC,
∴AO⊥平面CBB1C1.
由(1)可知OM∥平面CB1A1,
∴点M到平面CB1A1的距离等于点O到平面CB1A1的距离,设其为d,
在直三棱柱ABCA1B1C1中,由AB=AC=![]() ,BC=AA1=2可得,AO=1,A1B1=
,BC=AA1=2可得,AO=1,A1B1=![]() ,A1C=
,A1C=![]() ,B1C=
,B1C=![]() ,
,
∴△CB1A1是直角三角形,且![]() .
.
由![]() 得
得![]() ,
,
故d=![]() .即点M到平面CB1A1的距离为
.即点M到平面CB1A1的距离为![]() .
.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目