题目内容
1.“α≠$\frac{π}{3}$”是“cosα≠$\frac{1}{2}$”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
分析 根据充分条件和必要条件的定义进行判断即可.
解答 解:若α=-$\frac{π}{3}$,满足α≠$\frac{π}{3}$,但cosα=$\frac{1}{2}$,即cosα≠$\frac{1}{2}$不成立,即充分性不成立,
若cosα≠$\frac{1}{2}$,则α≠±$\frac{π}{3}$+2kπ,故α≠$\frac{π}{3}$成立,即必要性成立,
故“α≠$\frac{π}{3}$”是“cosα≠$\frac{1}{2}$”的必要不充分条件,
故选:B.
点评 本题主要考查充分条件和必要条件的判断,比较基础.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
20.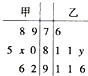 某中学高一级从甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是80,乙班学生成绩的中位数是89,则x+y的值为( )
某中学高一级从甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是80,乙班学生成绩的中位数是89,则x+y的值为( )
 某中学高一级从甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是80,乙班学生成绩的中位数是89,则x+y的值为( )
某中学高一级从甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是80,乙班学生成绩的中位数是89,则x+y的值为( )| A. | 7 | B. | 8 | C. | 9 | D. | 14 |
12.复平面上有点A,B其对应的复数分别为-3+i和-1-3i,O为原点,那么△AOB是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 正三角形 |
13.已知f1(x)=sinx,f2(x)=f1′(x),f3(x)=f2′(x),f4(x)=f3′(x),…,fn(x)=fn-1′(x),则f2015(x)等于( )
| A. | cosx | B. | -cosx | C. | sinx | D. | -sinx |