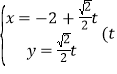题目内容
【题目】已知圆M：（x
）2+y2＝r2（r＞0）．若椭圆C：
1（a＞b＞0）的右顶点为圆M的圆心，离心率为
．
（1）求椭圆C的方程；
（2）若存在直线l：y＝kx，使得直线l与椭圆C分别交于A，B两点，与圆M分别交于G，H两点，点G在线段AB上，且|AG|＝|BH|，求圆M半径r的取值范围．
【答案】（1）
；（2）
．
【解析】
（1）由题判断可知，
，再结合离心率
和椭圆的关系式
即可求解；
（2）需要将题意进行转化，要求
其实也就是求
，联立直线与椭圆方程，求出弦长
，再由圆心到直线距离公式求出弦心距，结合几何关系表示出
，令可表示出
，由不等式的性质和函数关系即可求解
的取值范围；
（1）设椭圆的焦距为2c，
由椭圆右顶点为圆M的圆心（
，0），得a
，
又
，所以c＝1，b＝1．
所以椭圆C的方程为：
．
（2）设A（x1，y1），B（x2，y2），
由直线l与椭圆C交于两点A，B，则
，
所以（1+2k2）x2﹣2＝0，则x1+x2＝0，
，
所以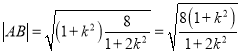
，
点M（，0）到直线l的距离d
，
则|GH|＝2
，
显然，若点H也在线段AB上，则由对称性可知，若直线y＝kx是y轴，矛盾，
所以要使|AG|＝|BH|，只要|AB|＝|GH|，
所以
4
，
2
，
当k＝0时，r，
当k≠0时，
2（1
）＝3，
又显然
2，所以
，
综上，．
【题目】某地随着经济的发展，居民收入逐年增长该地一建设银行统计连续五年的储蓄存款（年底余额）得到下表：
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
储蓄存款y（千亿元） | 5 | 6 | 7 | 8 | 10 |
为便于计算，工作人员将上表的数据进行了处理（令
），得到下表：
时间t | 1 | 2 | 3 | 4 | 5 |
储蓄存款z | 0 | 1 | 2 | 3 | 5 |
（1）求z关于t的线性回归方程；
（2）通过（1）中的方程，求出y关于x的回归方程；
（3）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？
附：线性回归方程
，其中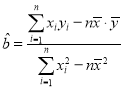
，
.
